Ми знаємо а дерево є нелінійною структурою даних. Він не має обмежень по кількості дітей. АЩо таке повне бінарне дерево?
Повне бінарне дерево — це особливий тип бінарного дерева, у якому всі рівні дерева заповнені повністю, за винятком вузлів найнижчого рівня, які заповнюються якомога ліворуч.

Повне бінарне дерево
Деяка термінологія повного бінарного дерева:
- Корінь – Вузол, в якому жодне ребро не походить від батьківського. Приклад - вузол А
- дитина – Вузол, що має деяке вхідне ребро, називається дочірнім. Приклад – вузли B, F є дочірніми вузлами A і C відповідно.
- рідний брат – Вузли, що мають одного батька, є однорідними. Приклад: D, E є рідними братами і сестрами, оскільки вони мають одного батька B.
- Ступінь вузла – Кількість дітей у певного батька. Приклад. Степінь A дорівнює 2, а ступінь C дорівнює 1. Ступінь D дорівнює 0.
- Внутрішні/зовнішні вузли – Листові вузли є зовнішніми вузлами, а нелистові вузли є внутрішніми вузлами.
- Рівень – Підраховуйте вузли на шляху до вузла призначення. Приклад. Рівень вузла D дорівнює 2, оскільки вузли A і B утворюють шлях.
- Висота – Кількість ребер для досягнення вузла призначення, корінь знаходиться на висоті 0. Приклад – висота вузла E дорівнює 2, оскільки він має два ребра від кореня.
Властивості повного бінарного дерева:
- Повне бінарне дерево називається правильним бінарним деревом, де всі листи мають однакову глибину.
- У повному двійковому дереві кількість вузлів на глибині d є 2 d .
- У повному бінарному дереві с п Висота вузлів дерева становить log(n+1) .
- Всі рівні крім останнього рівня повністю заповнені.
Ідеальне бінарне дерево проти повного бінарного дерева:
Бінарне дерево висотою «h» з максимальною кількістю вузлів є a ідеальний бінарне дерево.
Для заданої висоти ч , максимальна кількість вузлів становить 2 h+1 -1 .
А повний двійкове дерево висоти h є ідеальним бінарним деревом до висоти h-1 , і в останньому елементі рівня зберігаються в порядку зліва направо.
Приклад 1:
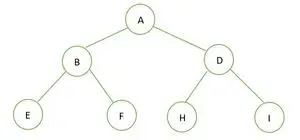
Бінарне дерево
Висота даного бінарного дерева дорівнює 2, а максимальна кількість вузлів у цьому дереві дорівнює n= 2h+1-1 = 22+1-1 = 23-1 = 7 .
Отже, ми можемо зробити висновок, що так ідеальне бінарне дерево .
Тепер повне бінарне дерево заповнене до висоти h-1 тобто; 1, а елементи останнього рівня зберігаються в порядку зліва направо. Отже, це також повне бінарне дерево. Ось представлення елементів, які зберігаються в масиві

Елемент, що зберігається в масиві рівень за рівнем
У масиві всі елементи зберігаються безперервно.
приклад 2:
сортування оболонки
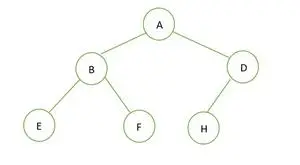
Бінарне дерево
Висота даного бінарного дерева дорівнює 2, а максимальна кількість вузлів, яка повинна бути там, дорівнює 2h+1– 1 = 22+1– 1 = 23– 1 = 7 .
Але кількість вузлів у дереві є 6 . Тому це так не ідеальне бінарне дерево .
Тепер повне бінарне дерево заповнене до висоти h-1 тобто; 1 і елемент останнього рівня зберігаються в порядку зліва направо. Отже, це a повне бінарне дерево . Збережіть елемент у масиві, і він буде таким;
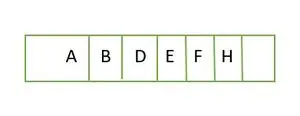
Елемент, що зберігається в масиві рівень за рівнем
приклад 3:
vba
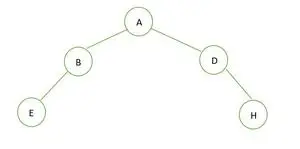
Бінарне дерево
Висота бінарного дерева дорівнює 2, а максимальна кількість вузлів, яка може бути там, становить 7, але є лише 5 вузлів, отже, це не ідеальне бінарне дерево .
У випадку повного бінарного дерева ми бачимо, що на останньому рівні елементи не заповнені зліва направо. Так воно і є не повне бінарне дерево .
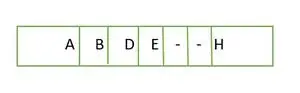
Елемент, що зберігається в масиві рівень за рівнем
Елементи в масиві не є безперервними.
Повне бінарне дерево проти повного бінарного дерева:
Для повного бінарного дерева кожен вузол має або 2 дітей, або 0 дітей.
Приклад 1:
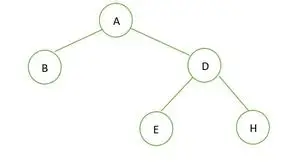
Бінарне дерево
У даному двійковому дереві немає вузла зі ступенем 1, або 2 або 0 дітей для кожного вузла, отже, це повне бінарне дерево .
Для повного бінарного дерева елементи зберігаються на рівні за рівнем, а не з крайньої лівої сторони останнього рівня. Тому це не повне бінарне дерево . Представлення масиву таке:
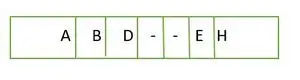
Елемент, що зберігається в масиві рівень за рівнем
приклад 2:
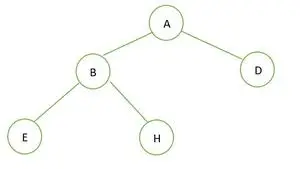
Бінарне дерево
У даному бінарному дереві немає вузла зі ступенем 1. Кожен вузол має ступінь 2 або 0. Отже, це повне бінарне дерево .
Для повного бінарного дерева елементи зберігаються порівневим способом і заповнюються з крайньої лівої сторони останнього рівня. Звідси це а повне бінарне дерево . Нижче представлено масив дерева:
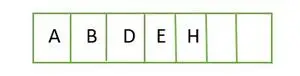
Елемент, що зберігається в масиві рівень за рівнем
приклад 3:
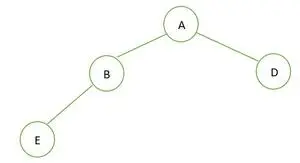
Бінарне дерево
У даному бінарному дереві вузол B має ступінь 1, що порушує властивість повного бінарного дерева, отже, це не повне бінарне дерево
рядок n java
Для повного бінарного дерева елементи зберігаються порівневим способом і заповнюються з крайньої лівої сторони останнього рівня. Отже, це a повне бінарне дерево . Представлення масиву бінарного дерева:
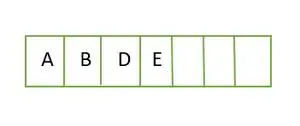
Елемент, що зберігається в масиві рівень за рівнем
Приклад 4:
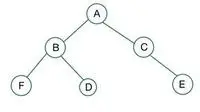
бінарне дерево
У даному бінарному дереві вузол C має ступінь 1, що порушує властивість повного бінарного дерева, отже, це не повне бінарне дерево
рядок формату java
Для повного бінарного дерева елементи зберігаються порівневим способом і заповнюються з крайньої лівої сторони останнього рівня. Тут вузол E порушує умову. Тому це не повне бінарне дерево .
Створення повного бінарного дерева:
Ми знаємо а повне бінарне дерево це дерево, в якому за винятком останнього рівня (скажімо л )усі інші рівні мають ( 2л ) вузли, а вузли вишикувані зліва направо.
Його можна представити за допомогою масиву. Якщо батьківський — це індекс i тому ліва дитина знаходиться на 2і+1 і права дитина знаходиться на 2і+2 .
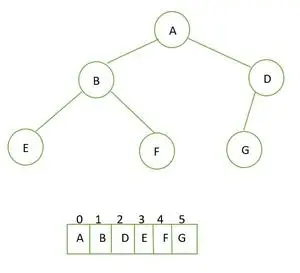
Повне бінарне дерево та його масив
Алгоритм:
Для створення а Повне бінарне дерево , ми вимагаємо a Крок 1: Ініціалізуйте корінь новим вузлом, коли дерево порожнє.
Крок 2: Якщо дерево не порожнє, тоді візьміть передній елемент
- Якщо передній елемент не має лівого дочірнього елемента, тоді встановіть лівий дочірній елемент на новий вузол
- Якщо правий дочірній елемент відсутній, установіть правий дочірній елемент як новий вузол
крок 3: Якщо вузол має обидва дочірні елементи, тоді поп це з черги.
крок 4: Поставте нові дані в чергу.
Ілюстрація:
Розглянемо наведений нижче масив:
1. Перший елемент буде коренем (значення за індексом = 0 )
перетворення об'єкта в рядокA береться як корінь
2. Наступний елемент (за індексом = 1 ) залишиться зліва, а третій елемент (індекс = 2 ) буде правильним дочірнім елементом root
B як ліва дитина, а D як права дитина
3. четвертий (індекс = 3 ) і п’ятий елемент (індекс = 4 ) буде лівим і правим дочірніми елементами вузла B
E і F є лівим і правим дочірніми елементами B
4. Наступний елемент (індекс = 5 ) залишиться нащадком вузла D
G стає лівим дочірнім елементом вузла D
Так створюється повне бінарне дерево.
Реалізація: Для реалізації побудови повного бінарного дерева з обходу порядку рівня наведено в цей пост .
Застосування повного бінарного дерева:
- Сортування купи
- Структура даних на основі сортування купи
Перевірте, чи дане двійкове дерево повне чи ні: Слідуйте цей пост щоб перевірити, чи дане двійкове дерево повне чи ні.




