Кут між двома векторами - це кут між їхніми хвостами, і цей кут можна легко знайти за допомогою перехресного добутку та скалярного добутку векторних формул. Кут між двома векторами завжди лежить між 0° і 180°.
У цій статті ми детально дізнаємось про кут між двома векторами, визначення, формули та приклади.
Що таке кут між двома векторами?
Кут між двома векторами - це кут, утворений при перетині їх хвостів. Кут між двома векторами може бути гострим, прямим або тупим залежно від напрямку векторів.
каджал аггарвал
Кут між двома векторами знаходять за двома формулами:
- Використання скалярного добутку векторів
- Використання перехресного добутку векторів
Це пояснюється у формулі нижче.
Формули кута між двома векторами
Кут між двома векторами легко і найчастіше знайдено за допомогою скалярного добутку векторів.

Два вектора A і B
Точковий добуток A і B визначається як
vec{A}.vec{B} = |A| |B| cosθ.
Особливі випадки
- Коли кут між векторами дорівнює 0 градусів.
Тобто θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Коли кут між векторами дорівнює 180 градусів.
⇒ |A| |B| cosθ
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Коли кут між векторами дорівнює 90 градусів.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Формула кута між двома векторами
Косинус кута між двома векторами дорівнює сумі добутку окремих складових двох векторів, поділеного на добуток величини двох векторів.
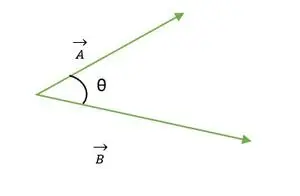
Два вектори A і B
cosθ=
θ= cos-1
У декартовій формі,
А = Ахi + Aіj + Aсk
B= Bхi + Bіj + Bсk
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Властивості скалярного добутку
- Скалярний добуток є комутативним
vec{A}.vec{B}=vec{B}.vec{A}
- Точковий продукт є розподільним
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
Кут між двома векторами лежить між 0 ≤ θ ≤ 180. Коли хвости або голови обох векторів збігаються, тоді обчислюється кут між векторами.
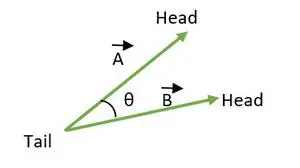
Хвіст збігається
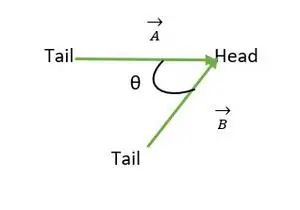
Голова збігається
Зразки задач Формула кута між двома векторами
Задача 1. Знайти кут між векторами (якщо вони утворюють рівносторонній трикутник)
- вектори a і b
- вектори b і c
- вектори a і c
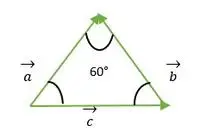
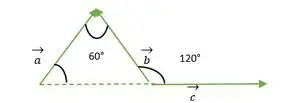
Рівносторонній трикутник, утворений векторами a, b, c
рішення:
- вектори a і b
Для вектора a і b вершини обох векторів збігаються, отже, кут між векторами a і b дорівнює куту між двома сторонами рівностороннього трикутника = 60°.
- вектори b і c:
З наведеного вище малюнка ми бачимо, що голова або хвіст вектора b і c не збігаються один з одним.
Отже, використовуючи властивість - вектор залишається незмінним, якщо він передається паралельно самому собі.
Вектор c зсувається паралельно самому собі
Тепер ми бачимо, що хвіст векторів b і c збігається один з одним, тому такий самий, як і зовнішній кут, складений із рівностороннім трикутником = 120°.
- вектори a і c
Хвіст a і c збігається
Для векторів a і c хвости обох векторів збігаються один з одним, тому кут між векторами a і c дорівнює куту між двома сторонами рівностороннього трикутника = 60°.
Завдання 2. Знайти кути між векторами, якщо вони утворюють рівнобедрений прямокутний трикутник.
- a і b вектор
- вектор b і c
- вектори a і c
рішення:
- a і b вектор
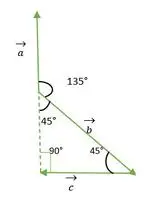
Рівнобедрений трикутник під прямим кутом
З наведеного вище малюнка ми бачимо, що голова або хвіст вектора a і b не збігаються один з одним. Отже, використовуючи властивість - вектор залишається незмінним, якщо він передається паралельно самому собі.
вектор зсувається паралельно самому собі
Тепер хвости векторів a і b збігаються один з одним і утворюють кут, такий же, як і зовнішній кут прямокутного рівнобедреного трикутника = 135°.
- вектор b і c
Рівнобедрений трикутник під прямим кутом
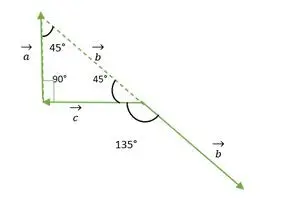
З наведеного вище малюнка голова або решка векторів b і c не збігаються один з одним. Отже, використовуючи властивість, вектор залишається незмінним, якщо він передається паралельно самому собі.
вектор b зсувається паралельно самому собі
перейменування папки в linuxТепер хвости векторів b і c збігаються один з одним і утворюють кут, такий же, як і зовнішній кут прямокутного рівнобедреного трикутника = 135°.
- вектори a і c
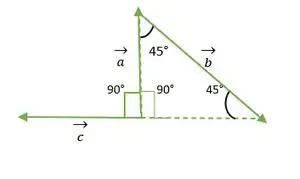
Рівнобедрений трикутник під прямим кутом
З наведеного вище малюнка голова або решка векторів a і c не збігаються один з одним. Отже, використовуючи властивість - вектор залишається незмінним, якщо він передається паралельно самому собі.
вектор c переміщується паралельно самому собі
Тепер хвости векторів a і c збігаються між собою і утворюють кут, такий же, як прямий кут рівнобедреного трикутника = 90°.
Задача 3: Знайти кут між векторами A = i + j + k і вектором B = -2i – 2j – 2k.
рішення:
З формули
А = Ахi + Aіj + Aсk
B= Bхi + Bіj + Bсk
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Тут у заданому питанні
A= i + j + k
B= -2i -2j -2k
Підстановка значень у формулу
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
Задача 4: Знайти кут між вектором A = 3i + 4j і B = 2i + j
рішення:
А = Ахi + Aіj + Aсk
B = Bхi + Bіj + Bсk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Тут Дано,
A= 3i + 4j + 0k
B= 2i + j + 0k
Підставляючи значення у формулу,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} linux free ipconfig⇒ θ = cos-1(
frac{(10)}{5.(sqrt{5})} )⇒ θ = cos-1(
frac{2}{(sqrt{5})} )
Задача 5: Знайти кут між вектором A = i + j і вектором B = j + k.
рішення:
З формули
А = Ахi + Aіj + Aсk
B = Bхi + Bіj + Bсk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Тут у заданому питанні
⇒ A = i + j
⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos-1(1/2)
⇒ θ = 60°