Топологічне сортування для Спрямований ациклічний граф (DAG) є лінійним упорядкуванням вершин таким, що для кожного спрямованого ребра u-v вершина в приходить раніше в в упорядкуванні.
Примітка: Топологічне сортування для графа неможливе, якщо граф не є a ДЕНЬ .
приклад:
Рекомендована практикаРішення на основі DFS для пошуку топологічного сортування вже обговорювалося.введення: Графік:
java, якщо іншеприклад
Вихід: 5 4 2 3 1 0
Пояснення: Перша вершина в топологічному сортуванні завжди є вершиною зі ступенем 0 (вершина без вхідних ребер). Топологічне сортування наступного графа дорівнює 5 4 2 3 1 0. Для графа може бути більше одного топологічного сортування. Іншим топологічним сортуванням наступного графа є 4 5 2 3 1 0.
Топологічний порядок може бути не унікальним:
Топологічне сортування це проблема залежності, в якій виконання одного завдання залежить від виконання кількох інших завдань, порядок яких може змінюватися. Розберемо цю концепцію на прикладі:
Припустимо, наше завдання - дійти до нашої школи, і щоб туди потрапити, нам спочатку потрібно одягнутися. Залежності від носіння одягу показано на графіку залежностей нижче. Наприклад, не можна одягати взуття, перш ніж одягнути шкарпетки.
З наведеного вище зображення ви вже зрозуміли, що існує кілька способів одягнутися, на зображенні нижче показано деякі з цих способів.
Чи можете ви перерахувати всі можливі топологічні впорядкування одягатися для наведеного вище графіка залежностей?
f-рядковий пітон
Алгоритм топологічного сортування за допомогою DFS:
Ось покроковий алгоритм топологічного сортування за допомогою пошуку спочатку в глибину (DFS):
- Створіть графік за допомогою п вершини і м -спрямовані ребра.
- Ініціалізувати стек і відвіданий масив розміром п .
- Для кожної невідвіданої вершини на графі виконайте такі дії:
- Викличте функцію DFS із вершиною як параметром.
- У функції DFS позначте вершину як відвідану та рекурсивно викличте функцію DFS для всіх невідвіданих сусідів вершини.
- Коли всі сусіди будуть відвідані, помістіть вершину в стек.
- Після того, як вершини були відвідані, витягніть елементи зі стеку та додайте їх до списку виводу, доки стек не буде порожнім.
- Отриманий список є топологічно відсортованим порядком графа.
Ілюстрація Алгоритм топологічного сортування:
Нижче зображено ілюстрацію описаного вище підходу:

Загальний робочий процес топологічного сортування
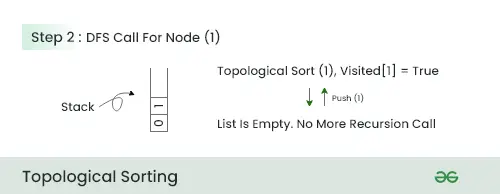
Крок 1:
- Ми запускаємо DFS з вузла 0, оскільки він не має нульових вхідних вузлів
- Ми поміщаємо вузол 0 у стек і переходимо до наступного вузла з мінімальною кількістю суміжних вузлів, тобто до вузла 1.
крок 2:
- На цьому кроці, оскільки немає суміжних вузлів, помістіть вузол 1 у стек і перейдіть до наступного вузла.
крок 3:
- На цьому кроці ми вибираємо вузол 2, оскільки він має мінімальну кількість суміжних вузлів після 0 і 1.
- Ми викликаємо DFS для вузла 2 і надсилаємо всі вузли, які надходять у обхід від вузла 2, у зворотному порядку.
- Тож натисніть 3, потім натисніть 2.
windows.open javascriptкрок 4:
- Тепер ми викликаємо DFS для вузла 4
- Оскільки 0 і 1 уже присутні в стеку, ми просто вставляємо вузол 4 у стек і повертаємося.
крок 5:
- На цьому кроці, оскільки всі суміжні вузли 5 уже знаходяться в стеку, ми вставляємо вузол 5 у стек і повертаємося.
Крок 6: Це останній крок топологічного сортування, під час якого ми виймаємо всі елементи зі стеку та друкуємо їх у такому порядку.
Нижче наведено реалізацію вищезазначеного підходу:
простий форматування дати в javaC++
#include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& присл., вектор & відвідав, стек & Stack) { // Позначити поточний вузол як відвіданий visited[v] = true; // Повторюється для всіх суміжних вершин for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Надішліть поточну вершину до стеку, який зберігає результат Stack.push(v); } // Функція для виконання топологічного сортування void topologicalSort(vector>& adj, int V) { стек стек; // Стек для зберігання вектора результату відвідав (V, false); // Виклик рекурсивної допоміжної функції для збереження // Топологічного сортування, починаючи з усіх вершин одну за // однією для (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> ребра = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Граф, представлений як вектор списку суміжності> adj(V); for (auto i : edges) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, boolean[] відвідав, стек stack) { // Позначити поточний вузол як відвіданий visited[v] = true; // Повторюється для всіх суміжних вершин for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Надішліть поточну вершину до стеку, який // зберігає результат stack.push(v); } // Функція для виконання топологічного сортування static void topologicalSort(List> adj, int V) { // Стек для збереження результату Стек стек = новий стек(); boolean[] відвідано = новий boolean[V]; // Виклик рекурсивної допоміжної функції для збереження // Топологічного сортування, починаючи з усіх вершин по одній // для (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> edges = new ArrayList(); edges.add(Arrays.asList(0, 1)); edges.add(Arrays.asList(1, 2)); edges.add(Arrays.asList(3, 1)); edges.add(Arrays.asList(3, 2)); // Граф представлений як список суміжності List> adj = новий ArrayList(V); для (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : краї) { adj.get(i.get(0)).add(i.get(1)); } topologicalSort(adj, V); } }>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] відвідав, стек stack) { // Позначити поточний вузол як відвіданий visited[v] = true; // Повторюється для всіх суміжних вершин foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Надішліть поточну вершину до стеку, який зберігає // результат stack.Push(v); } // Функція для виконання топологічного сортування static void TopologicalSort(List> adj, int V) { // Стек для збереження результату Стек стек = новий стек (); bool[] відвідано = новий bool[V]; // Виклик рекурсивної допоміжної функції для збереження // Топологічного сортування, починаючи з усіх вершин по одній // для (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Код драйвера static void Main(string[] args) { // Кількість вузлів int V = 4; // Список ребер> edges = новий список>{ новий список { 0, 1 }, новий список { 1, 2 }, новий список { 3, 1 }, новий список { 3, 2 } }; // Граф представлений як список суміжності List> adj = новий список>(); для (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Список i в краях) { adj[i[0]].Add(i[1]); } TopologicalSort(adj, V); } }>
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // Код драйвера (() => { // Кількість вузлів const V = 4; // Ребра const edges = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Граф представлений як список суміжності const adj = Array.from({ length: V }, () => []); for (let i of edges) { adj[i[0]].push (i[1]) topologicalSort(adj, V)();> Вихід
Topological sorting of the graph: 3 0 1 2>
Часова складність: O(V+E). Наведений вище алгоритм — це просто DFS із додатковим стеком. Отже, часова складність така ж, як і DFS
Допоміжні приміщення: O(V). Для стосу потрібен додатковий простір
Топологічне сортування за допомогою BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * присл. // Покажчик на масив, що містить // списки суміжності public: Graph(int V); // Конструктор void addEdge(int v, int w); // Функція для додавання ребра до графіка void topologicalSort(); // друкує топологічний сорт // повного графа }; Graph::Graph(int V) { this->V = V; adj = новий список [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Додати w до списку v. } // Функція для виконання топологічного сортування void Graph::topologicalSort() { // Створення вектора для збереження вектора в ступені всіх вершин in_degree(V, 0); // Огляд списків суміжності для заповнення in_degree // вершин для (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; для (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Одна за одною виключає вершини з черги та з черги // суміжні вершини, якщо ступінь суміжних стає 0 while (!q.empty()) { // Витягти початок черги (або виконати вилучення з черги) // і додати його до топологічний порядок int u = q.front(); q.pop(); top_order.push_back(u); // Ітерація по всіх сусідніх вузлах // вилученого з черги вузла u та зменшення їхнього ступеня // на 1 список ::ітератор itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Якщо in-degree стає нульовим, додайте його до черги if (--in_degree[*itr) ] == 0) q.push(*itr); рахувати++; } // Перевірити, чи був цикл if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] присл.; // Список суміжності // представлення // графа // Конструктор Graph(int V) { this.V = V; adj = новий ArrayList[V]; для (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = новий LinkedList(); для (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = новий ArrayList(); // Одна за одною вилучає вершини з черги та // ставить у чергу суміжні вершини, якщо в ступені // сусідня стає 0 while (!q.isEmpty()) { // Витягти передню частину черги та додати її до // топологічного порядку int u = q.poll(); topOrder.add(u); рахувати++; // Перебираємо всі сусідні вузли // вилученого з черги вузла u та зменшуємо їхню ступінь // на 1 for (int w : adj[u]) { // Якщо ступінь стає нульовою, // додаємо її до черги if (--inDegree[w] == 0) q.add(w); } } // Перевірити, чи був цикл if (count != V) { System.out.println('Графік містить цикл'); повернення; } // Вивести топологічний порядок для (int i : topOrder) System.out.print(i + ' '); } } // Код драйвера public class Main { public static void main(String[] args) { // Створіть графік, наведений на діаграмі вище Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Далі є топологічний сорт даного графа'); g.topologicalSort(); } }> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Вихід
Following is a Topological Sort of the given graph 4 5 2 0 3 1>
Часова складність:
Часова складність побудови графа дорівнює O(V + E), де V – кількість вершин, E – кількість ребер.
Часова складність для виконання топологічного сортування за допомогою BFS також дорівнює O(V + E), де V — кількість вершин, а E — кількість ребер. Це тому, що кожна вершина та кожне ребро відвідуються один раз під час обходу BFS.
Космічна складність:
Складність простору для зберігання графа за допомогою списку суміжності становить O(V + E), де V — кількість вершин, а E — кількість ребер.
фон css
Додатковий простір використовується для зберігання ступеня вершин, для чого потрібен простір O(V).
Для обходу BFS використовується черга, яка може містити не більше V вершин. Таким чином, складність простору для черги дорівнює O(V).
Загалом, просторова складність алгоритму становить O(V + E) через зберігання графа, масиву за ступенем і черги.
Підсумовуючи, часова складність наданої реалізації становить O(V + E), а просторова складність також O(V + E).
Примітка: Тут ми також можемо використовувати масив замість стека. Якщо використовується масив, надрукуйте елементи у зворотному порядку, щоб отримати топологічне сортування.
Переваги топологічного сортування:
- Допомагає планувати завдання або події на основі залежностей.
- Виявляє цикли в орієнтованому графі.
- Ефективний для вирішення проблем з обмеженнями пріоритету.
Недоліки топологічного сортування:
- Застосовується лише до спрямованих ациклічних графів (DAG), не підходить для циклічних графів.
- Може бути не унікальним, може існувати кілька дійсних топологічних порядків.
- Неефективний для великих графів із багатьма вузлами та ребрами.
Застосування топологічного сортування:
- Планування завдань і управління проектами.
- Вирішення залежностей у системах керування пакетами.
- Визначення порядку компіляції в системах побудови програмного забезпечення.
- Виявлення взаємоблокувань в операційних системах.
- Розклад курсів у ВНЗ.
Схожі статті:
- Алгоритм Кана для топологічного сортування
- Усі топологічні сорти орієнтованого ациклічного графа