Площа поверхні призми: У математиці призма є важливим членом сімейства багатогранників і визначається як тривимірна форма, що складається з двох однакових багатокутників, звернених один до одного, з’єднаних збоку прямокутними або паралелограмними гранями. Однакові багатокутники можуть бути трикутниками, квадратами, прямокутниками, п’ятикутниками або будь-якими іншими n-сторонніми многокутниками і називаються основами призми. Інші грані призми — паралелограми або прямокутники.
У цій статті ми обговоримо різні типи призм і формула площі поверхні призми з прикладами та практичними завданнями.
Зміст
- Що таке площа поверхні призми?
- Різні типи призм
- Формула площі поверхні призми
- Розв’язані приклади площі поверхні призми
- Тренувальні задачі на площу поверхні призми
Що таке площа поверхні призми?
Площею поверхні призми називають загальну площу, яку охоплюють усі її грані. Щоб визначити площу поверхні призми, потрібно обчислити площі кожної з її граней, а потім скласти отримані площі. Призма має два види площі поверхні, а саме площу бічної поверхні та загальну площу поверхні. Площа, зайнята гранями призми, за винятком двох паралельних граней (основ призми), називається площею її бічної поверхні.
помилка: не вдалося знайти або завантажити основний клас
Площа бічної поверхні призми = [периметр основи × висота] квадратних одиниць
Тепер загальна площа поверхні призми дорівнює сумі площ двох її основ і площі бічної поверхні.
Загальна формула для обчислення повної площі поверхні будь-якого типу прямої призми:
Загальна площа поверхні призми = [2 (площа основи) + (периметр основи × висота)] квадратних одиниць
Різні типи призм
Існують різні типи призм залежно від форми основи призми, наприклад
- Трикутні призми,
- квадратні призми,
- Прямокутні призми,
- п'ятикутні призми,
- шестикутні призми,
- Восьмикутні призми.
Трикутна призма
Призму з трикутною основою називають трикутною призмою. Трикутна призма складається з трьох похилих прямокутних поверхонь і двох паралельних основ трикутника. Нехай Н — висота трикутної призми; a, b, c — довжини сторін, h — висота основ трикутника.
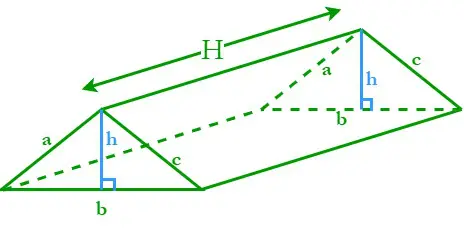
Периметр трикутної основи (P) = сума трьох його сторін = a + b + c
Площа трикутної основи (A) = ½ × основа × висота = ½ bh
Ми знаємо, що загальна формула для площа бічної поверхні прямої призми L. S. A. = PH, де P — периметр основи, а A — площа основи.
Підставляючи всі значення в загальну формулу отримуємо ,
Площа бічної поверхні трикутної призми = (a + b +c)H квадратних одиниць
де,
a, b, c — сторони основи трикутника
Н - висота трикутної призми
Ми знаємо, що загальна формула для повної площі поверхні прямої призми така T. S. A. = PH+2A, де P — периметр основи, A — площа основи, а H — висота призми.
Підставляючи всі значення в загальну формулу отримуємо
Загальна площа поверхні трикутної призми = (a + b + c)H + 2 × (½ bh)
Загальна площа поверхні трикутної призми = (a + b + c)H + bh квадратних одиниць
де,
a, b, c — сторони основи трикутника
Н - висота трикутної призми
h - висота трикутника
Прямокутна призма
Призму з прямокутною основою називають прямокутною призмою. Прямокутна призма складається з чотирьох прямокутних поверхонь і двох паралельних прямокутних основ. Нехай висота призми дорівнює h, а довжина і ширина її прямокутних основ дорівнюють l і w відповідно .

Периметр прямокутної основи (P) = Сума його чотирьох сторін = 2 (l + w)
Площа прямокутної основи (A) = довжина × ширина = довжина × ширина
Ми знаємо, що загальна формула для площі бічної поверхні прямої призми така: L. S. A. = PH, де P — периметр основи, а A — площа основи.
Підставляючи всі значення в загальну формулу отримуємо ,
Площа бічної поверхні прямокутної призми = 2h(l + w) квадратних одиниць
де,
l - довжина
w - ширина
h - висота
Ми знаємо, що загальна формула для повної площі поверхні прямої призми: T. S. A. = PH+2A, де P — периметр основи, A — площа основи, а H — висота призми.
Підставляючи всі значення в загальну формулу отримуємо
Загальна площа поверхні прямокутної призми = 2h(l + w) + 2(l × w)
= 2 lh + 2 wh + 2 lw
Загальна площа поверхні прямокутної призми = 2 (lh + wh + lw) квадратних одиниць
де,
l - довжина
w - ширина
h - висота
Квадратна призма
Призму з квадратною основою називають квадратною призмою. Квадратна призма складається з чотирьох прямокутних поверхонь і двох паралельних квадратних основ. Нехай висота призми дорівнює h, а довжини її квадратних основ s.

Периметр квадрата з основою (P) = Сума його чотирьох сторін = s + s + s + s = 4s
Площа основи квадрата (A) = (довжина сторони)2= s2
Ми знаємо, що загальна формула для площі бічної поверхні прямої призми така: L. S. A. = PH, де P — периметр основи, а A — площа основи.
Підставивши всі значення в загальну формулу, отримаємо
Площа бічної поверхні квадратної призми = 4 квадратних одиниць
де,
s — сторона основи квадрата
h - висота квадратної призми
Ми знаємо, що загальна формула для повної площі поверхні прямої призми така T.S.A. = PH+2A, де P — периметр основи, A — площа основи, H — висота призми.
Підставивши всі значення в загальну формулу, отримаємо
Загальна площа поверхні квадратної призми = [4sh + 2s 2 ] квадратних одиниць
де,
s — сторона основи квадрата
h - висота квадратної призми
П'ятикутна призма
Призму з п'ятикутною основою називають п'ятикутною призмою. П'ятикутна призма складається з п'яти похилих прямокутних поверхонь і двох паралельних п'ятикутних основ. Нехай h — висота п’ятикутної призми; a і b — довжини апофем і довжини сторін основ п’ятикутників.

Периметр основи п’ятикутника (P) = сума його п’яти сторін = 5b
Площа основи п'ятикутника (A) = 5/2 x (довжина апофеми) x (довжина бічної сторони) = 5ab
Ми знаємо, що загальна формула для площі бічної поверхні прямої призми така: L. S. A. = PH, де P — периметр основи, а A — площа основи.
Підставивши всі значення в загальну формулу, отримаємо
Площа бічної поверхні п’ятикутної призми = 5bh квадратних одиниць
де,
b — сторона основи п’ятикутника
h - висота п'ятикутної призми
Ми знаємо, що загальна формула для повної площі поверхні прямої призми: T. S. A. = PH+2A, де P — периметр основи, A — площа основи, а H — висота призми.
Підставивши всі значення в загальну формулу, отримаємо
Загальна площа поверхні п’ятикутної призми = [5bh + 5ab] квадратних одиниць
де,
b — сторона основи п’ятикутника
a — довжина апофеми.
h - висота п'ятикутної призми
Шестикутна призма
Призму з шестикутною основою називають шестикутною призмою. Шестикутна призма складається з шести похилих прямокутних поверхонь і двох паралельних шестикутних основ. Нехай h — висота шестикутної призми; a — довжини сторін основ шестикутника.

Периметр основи шестикутника (P) = сума шести його сторін = 6a
Площа основи шестикутника (A) = 6 х (площа рівностороннього трикутника)
A = 6 x (√3a2/4) ⇒ A = 3√3a2/2
Ми знаємо, що загальна формула для площі бічної поверхні прямої призми така: L. S. A. = PH, де P — периметр основи, а A — площа основи.
Підставивши всі значення в загальну формулу, отримаємо
Площа бічної поверхні шестикутної призми = 6ah квадратних одиниць
де,
a — сторона основи шестикутника
h – висота шестикутної основи
Ми знаємо, що загальна формула для повної площі поверхні прямої призми: T. S. A. = PH+2A, де P — периметр основи, A — площа основи, а H — висота призми.
Підставляючи всі значення в загальну формулу отримуємо
Загальна площа поверхні шестикутної призми = [6ah +3√3a2] квадратних одиниць
де,
a — сторона основи шестикутника
h - висота шестикутної основи:
Формула площі поверхні призми
У наведеній нижче таблиці наведено формули для різних типів призм:
Форма | Основа призми | Площа бічної поверхні[Периметр основи × висота] | Загальна площа поверхні[(2 × площа основи) + (периметр основи × висота)] |
|---|---|---|---|
Трикутна призма | Трикутник | (a + b +c)H квадратних одиниць | (a + b + c)H + bh квадратних одиниць |
Прямокутна призма | Прямокутник | 2h(l + w) квадратних одиниць | 2 (lh + wh + lw) квадратних одиниць |
Квадратна призма | Майдан | 4sh квадратних одиниць | [4ш + 2с2] квадратних одиниць |
П'ятикутна призма | П'ятикутник | 5bh квадратних одиниць | [5ab + 5bh] квадратних одиниць |
Шестикутна призма | Шестикутник | 6ah квадратних одиниць | [3√3a2+ 6ah] квадратних одиниць |
Розв’язані приклади площі поверхні призми
Задача 1: Яка висота призми, площа основи якої становить 36 квадратних одиниць, периметр основи — 24 одиниці, а загальна площа поверхні — 320 квадратних одиниць?
рішення:
Дані дані,
Базова площа = 36 квадратних одиниць
Периметр основи = 24 одиниці
Загальна площа поверхні призми = 320 квадратних одиниць
Ми маємо,
Загальна площа поверхні призми = (2 × площа основи) + (периметр основи × висота)
⇒ 320 = (2 × 36)+ (24 × год)
⇒ 24 год = 248 ⇒ год = 10,34 одиниць
Отже, висота даної призми дорівнює 10,34 одиниць.
Завдання 2: Знайти повну площу поверхні квадратної призми, якщо висота призми і довжина сторони квадратної основи дорівнюють 13 см і 4 см відповідно.
рішення:
Дані дані,
Висота квадратної призми (h) = 13 см
Довжина сторони основи квадрата (а) = 4 см
ми це знаємо,
Загальна площа поверхні квадратної призми = 2а2+ 4 год
= 2 × (4)2+ 4 × 4 × 13
= 32 + 208 = 240 см2
базова смуга проти широкосмуговоїОтже, повна площа поверхні даної призми 240 кв.см.
Завдання 3: Визначте довжину основи п’ятикутної призми, якщо її загальна площа становить 100 квадратних одиниць, а її висота та довжина апофеми дорівнюють 8 одиницям і 5 одиницям відповідно.
рішення:
Дані дані,
Загальна площа поверхні п’ятикутної призми = 100 квадратних одиниць
Висота призми (h) = 8 од
Довжина апофеми (а) = 5 одиниць
ми це знаємо,
Загальна площа поверхні п’ятикутної призми = 5ab + 5bh
⇒ 100 = 5b (a+ h)
⇒ 100/5 = b (5 + 8)
⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 одиниці
Отже, довжина основи дорівнює 1,54 одиниці
Проблема 4: Визначте висоту прямокутної призми і повну площу прямокутної призми, якщо площа її бічної поверхні дорівнює 540 см2, а довжина і ширина основи дорівнюють відповідно 13 см і 7 см.
рішення:
Дані дані,
Довжина прямокутної основи (l) = 13 см
Ширина прямокутної основи (ш) = 7 см
Площа бічної поверхні призми = 540 кв.см
Ми маємо,
Площа бічної поверхні призми = периметр основи × висота
⇒ 540 = 2 (довжина + ширина) висота
⇒ 2 (13 + 7) h = 540
⇒ 2 (20) h = 540 ⇒ h = 13,5 см
ми це знаємо,
Загальна площа поверхні прямокутної призми = 2 (lw + wh + lh)
= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))
= 2 × (91 + 94,5 + 175,5) = 722 кв. см
Отже, висота і площа повної поверхні даної прямокутної призми дорівнюють відповідно 13,5 см і 722 кв.
Задача 5: Визначте площу поверхні правильної шестикутної призми, якщо висота призми дорівнює 12 дюймів, а довжина сторони основи дорівнює 5 дюймів.
рішення:
Дані дані,
Висота призми (h) = 12 дюймів
Довжина сторони основи (a) = 6 дюймів
Площа поверхні правильної шестикутної призми = 6ah + 3√3a2
= 6 × 5 × 12 + 3√3(5)2
= 360 + 75√3
= 360 + 75 × (1,732) = 489,9 квадратних дюймів
Отже, площа поверхні даної призми становить 489,9 кв.
Задача 6: Обчисліть площі бічної та повної поверхні трикутної призми, периметр основи якої дорівнює 25 дюймів, довжина основи та висота трикутника дорівнюють 9 дюймів і 10 дюймів, а висота призми дорівнює 14 дюймів.
рішення:
Дані дані,
Висота призми (H) = 14 дюймів
Периметр основи призми (P) = 25 дюймів
Довжина основи трикутника = 9 дюймів
Висота трикутника = 10 дюймів
ми це знаємо,
Площа бічної поверхні призми = периметр основи × висота
= 25 × 14 = 350 кв
java подвійний до рядкаПлоща трикутної основи (A) = ½ × основа × висота = 1/2 × 9 × 10 = 45 квадратних дюймів
Загальна площа поверхні трикутної призми = 2A + PH
= 2 × 45 + 25 × 14 = 90 + 350 = 440 кв. дюймів
Отже, площі бічної та повної поверхні призми становлять 350 кв. дюймів і 440 кв. дюймів відповідно.
Тренувальні задачі на площу поверхні призми
1. Дано прямокутну призму з розмірами:
- Довжина = 6 см
- Ширина = 4 см
- Висота = 5 см
Обчисліть загальну площу поверхні.
2. Розглянемо трикутну призму з розмірами:
- Основа трикутника = 8 см
- Висота трикутника = 6 см
- Довжина призми = 10 см
Знайти повну площу поверхні.
3. Визначити площу поверхні правильної п’ятикутної призми за:
- Довжина сторони основи = 7 см
- Висота призми = 9 см.
4. Обчисліть площу поверхні шестикутної призми за допомогою:
- Довжина сторони основи правильного шестикутника = 10 см
- Висота призми = 12 см.
Площа поверхні призми – поширені запитання
Що таке призма в геометрії?
Призма — це тривимірна фігура з двома рівномірними паралельними основами та з’єднуючими їх бічними гранями прямокутника або паралелограма. Призми бувають різних форм, наприклад прямокутні призми, трикутні призми та п’ятикутні призми, кожна з яких має унікальні характеристики.
Як знайти площу поверхні призми?
Щоб знайти площу поверхні призми, обчисліть площі всіх її граней і потім підсумуйте їх. Для прямокутної призми формула площі поверхні дорівнює 2lw + 2lh + 2wh, де l — довжина, w — ширина, h — висота. Для інших типів призм, таких як трикутні або п’ятикутні призми, можуть знадобитися додаткові формули для площі основи та бічної площі.
Які властивості має призма?
Призми мають кілька ключових властивостей:
- Вони мають дві конгруентні паралельні основи.
- Усі бічні грані — паралелограми.
- Висота над рівнем моря - це перпендикулярна відстань між двома основами.
- Основи однакові за формою та розміром.
- Поперечний переріз, паралельний основам, завжди має ту саму форму і розмір, що й основи.
Які реальні приклади призм?
Призми можна знайти в різних повсякденних предметах і конструкціях. Приклади:
- Прямокутні призми: Будівлі, ящики з крупами, книги.
- Трикутні призми: дахи будинків, клиноподібні предмети.
- П'ятикутні призми: деякі типи колон, окремі архітектурні споруди.
- Шестикутні призми: певні типи кристалів, деякі пакувальні контейнери.
Чому площа поверхні важлива для призм?
Площа поверхні має вирішальне значення для призм, оскільки вона представляє загальну площу всіх поверхонь (граней) призми. Розуміння площі поверхні допомагає в різних практичних застосуваннях, таких як обчислення кількості матеріалу, необхідного для створення або покриття призмоподібного об’єкта, визначення швидкості теплопередачі та оптимізації дизайну упаковки.
