Стандартна форма параболи - y = ax2+ bx + c, де a, b і c — дійсні числа, а a не дорівнює нулю. Парабола визначається як множина всіх точок на площині, рівновіддалених від фіксованої прямої та фіксованої точки на площині.
У цій статті ми детально розберемо, що таке парабола, стандартне рівняння параболи, відповідні приклади та інші.
Зміст
Що таке парабола?
Парабола — це конічний переріз, визначений як сукупність усіх точок, рівновіддалених від точки, яка називається фокусом, і лінії, яка називається директрисою. Стандартні рівняння для параболи залежать від її орієнтації (напрямку відкриття) і положення.
Рівняння параболи
Рівняння параболи можна записати в стандартній або загальній формі, і обидва вони додаються нижче:
Загальні рівняння параболи
Загальне рівняння параболи таке:
y = 4a(x – h) 2 + k
(або)
x = 4a(y – k) 2 + год
Де (h, k) — вершина параболи.
Стандартні рівняння параболи
Стандартне рівняння параболи таке:
y = ax 2 + bx + c
(або)
х = є 2 + від + c
де a ніколи не може дорівнювати нулю.
Частини параболи
Деякі важливі терміни та частини параболи:
- Фокус: Фокус — це нерухома точка параболи.
- Директриса: Директриса параболи — це пряма, перпендикулярна до осі параболи.
- Фокусна акорда: Хорда, яка проходить через фокус параболи, перетинаючи параболу в двох різних точках, називається фокальною хордою.
- Фокусна відстань: Фокусна відстань - це відстань точки (x1, і1) на параболі від фокуса.
- Права сторона: Широка пряма кишка - це фокальна хорда, яка проходить через фокус параболи і перпендикулярна до осі параболи. Довжина широкого м’яза прямої кишки LL’ = 4a.
- Ексцентриситет: Відношення відстані точки від фокуса до її відстані від директриси називається ексцентриситетом (e). Для параболи ексцентриситет дорівнює 1, тобто e = 1.
Парабола має чотири стандартні рівняння, засновані на орієнтації параболи та її осі. Кожна парабола має різну поперечну вісь і сполучену вісь.
| Рівняння параболи | Парабола | Формули параметрів параболи |
|---|---|---|
| і 2 = 4 ах | 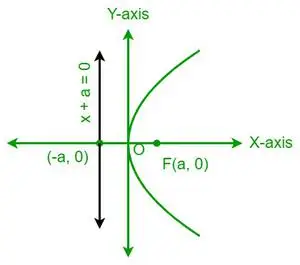 Горизонтальна парабола |
|
| і 2 = -4ax |  Горизонтальна парабола |
|
| х 2 = 4ay |  Вертикальна парабола |
|
| х 2 = -4ay |  Вертикальна парабола |
|
Нижче наведено спостереження, зроблені на основі стандартної форми рівнянь параболи:
- Парабола симетрична відносно своєї осі. Наприклад, у2= 4ax є симетричним відносно осі x, тоді як x2= 4ay є симетричним відносно осі y.
- Якщо парабола симетрична відносно осі х, то парабола відкривається вправо, якщо коефіцієнт х додатний, і вліво, якщо коефіцієнт х від’ємний.
- Якщо парабола симетрична відносно осі y, то парабола відкривається вгору, якщо y-коефіцієнт додатний, і вниз, якщо y-коефіцієнт від’ємний.
Нижче наведено стандартні рівняння параболи, коли вісь симетрії паралельна осі x або осі y, а вершина не знаходиться в початку координат.
| Рівняння параболи | Парабола | Формули параметрів параболи |
|---|---|---|
| (і – k)2= 4a(x – h) |  Горизонтальна парабола |
|
| (і – k)2= -4a(x – h) |  Горизонтальна парабола |
|
| (x – h)2= 4a(y – k) |  Вертикальна парабола |
|
| (x – h)2= -4a(y – k) |  Вертикальна парабола |
|
Рівняння похідної параболи
Нехай P — точка на параболі з координатами (x, y). З визначення параболи відстань точки P до фокуса (F) дорівнює відстані тієї ж точки P до директриси параболи. Тепер розглянемо точку X на директрисі, координати якої дорівнюють (-a, y).
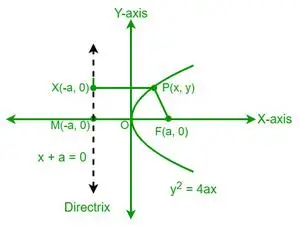
З визначення ексцентриситету параболи маємо
e = PF/PX = 1
⇒ PF = PX
Координати фокуса дорівнюють (a, 0). Тепер, використовуючи формулу координатної відстані, ми можемо знайти відстань точки P (x, y) до фокуса F (a, 0).
PF = √[(x – a)2+ (і – 0)2]
⇒ PF = √[(x – a)2+ і2] ------ (1)
Рівняння директриси x + a = 0. Щоб знайти відстань PX, ми використовуємо формулу перпендикулярної відстані.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
Ми вже знаємо, що PF = PX. Отже, прирівняйте рівняння (1) і (2).
√[(x – a)2+ і2] = (x + a)
Зводячи обидві сторони в квадрат ми отримуємо,
⇒ [(x – a)2+ і2] = (x + a)2
⇒ x2+ а2– 2ax + y2= х2+ а2+ 2 ос
⇒ і2– 2x = 2x
⇒ і2= 2ax + 2ax ⇒ і 2 = 4 ах
Отже, ми вивели рівняння параболи. Подібним чином ми можемо вивести стандартні рівняння трьох інших парабол.
- і2= -4ax
- х2= 4ay
- х2= -4ay
і 2 = 4ax, і 2 = -4ax, x 2 = 4ay і x 2 = -4ay є стандартними рівняннями параболи.
Статті, пов'язані з параболою:
- Рівняння кола
- Рівняння еліпса
- Рівняння гіперболи
- Застосування параболи в реальному житті
Приклади на рівняння параболи
Приклад 1. Знайдіть довжину прямої кишки, фокуса та вершини, якщо рівняння параболи дорівнює y 2 = 12x.
рішення:
враховуючи,
Рівняння параболи є у2= 12x
Порівнюючи задане рівняння зі стандартною формою y2= 4 ах
4a = 12
⇒ a = 12/4 = 3
ми це знаємо,
Права сторона параболи = 4a = 4 (3) = 12
Тепер фокус параболи = (a, 0) = (3, 0)
Вершина даної параболи = (0, 0)
Приклад 2: Знайдіть рівняння параболи, яка симетрична відносно осі Х і проходить через точку (-4, 5).
рішення:
враховуючи,
Парабола симетрична відносно осі Х і має вершину в початку координат.
Таким чином, рівняння може мати вигляд у2= 4ax або y2= -4ax, де знак залежить від того, в ліву чи праву сторону відкривається парабола.
Парабола має відкриватися вліво, оскільки вона проходить через (-4, 5), що лежить у другому квадранті.
Отже, рівняння буде таким: y2= -4ax
Підставивши (-4, 5) у наведене вище рівняння,
⇒ (5)2= -4a(-4)
⇒ 25 = 16а
⇒ a = 25/16
Отже, рівняння параболи має вигляд: y2= -4(25/16)x (або) 4y2= -25x.
Приклад 3. Знайти координати фокуса, осі, рівняння директриси та прямої широти параболи x 2 = 16 років.
рішення:
враховуючи,
Рівняння параболи має вигляд: x2= 16 років
Порівнюючи задане рівняння зі стандартною формою x2= 4ay,
4a = 16 ⇒ a = 4
Коефіцієнт y додатний, тому парабола відкривається вгору.
Крім того, вісь симетрії знаходиться вздовж позитивної осі Y.
Отже,
Фокус параболи (a, 0) = (4, 0).
Рівняння директриси має вигляд y = -a, тобто y = -4 або y + 4 = 0.
Довжина широкого м'яза прямої кишки = 4a = 4(4) = 16.
Приклад 4: Знайдіть довжину широти прямої кишки, фокуса та вершини, якщо рівняння параболи дорівнює 2(x-2) 2 + 16 = у.
рішення:
враховуючи,
Рівняння параболи дорівнює 2(x-2)2+ 16 = і
Порівнюючи задане рівняння із загальним рівнянням параболи y = a(x – h)2+ k, отримуємо
а = 2
(h, k) = (2, 16)
ми це знаємо,
Довжина прямої кишки параболи = 4а
= 4(2) = 8
Тепер фокус = (a, 0) = (2, 0)
Тепер Вершина = (2, 16)
Приклад 5: Рівняння параболи дорівнює x 2 – 12x + 4y – 24 = 0, потім знайдіть його вершину, фокус і директрису.
рішення:
враховуючи,
Рівняння параболи дорівнює x2– 12x + 4y – 24 = 0
⇒ x2– 12x + 36 – 36 + 4y – 24 = 0
⇒ (x – 6)2+ 4y – 60 = 0
⇒ (x – 6)2= -4(y + 15)
Отримане рівняння має вигляд (x – h)2= -4a(y – k)
-4a = -4 ⇒ a = 1
Отже, вершина = (h, k) = (6, – 15)
Фокус = (h, k – a) = (6, -15-1) = (6, -16)
Рівняння директриси має вигляд y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
Поширені запитання щодо рівняння параболи
Як знайти стандартне рівняння параболи?
Стандартною формою параболи є y2= 4ax або x2= 4ay.
Що таке нормальне рівняння параболи?
Рівняння нормалі до параболи у2= 4ax з нахилом m задається як: y = mx – 2am – am 3
Як знайти вершину параболи?
Для заданої параболи: y = ax2+ bx + c його вершину можна знайти за формулою x = − b/2a. Підставте це значення x назад у рівняння, щоб знайти відповідну координату y.
змагальний обшук
