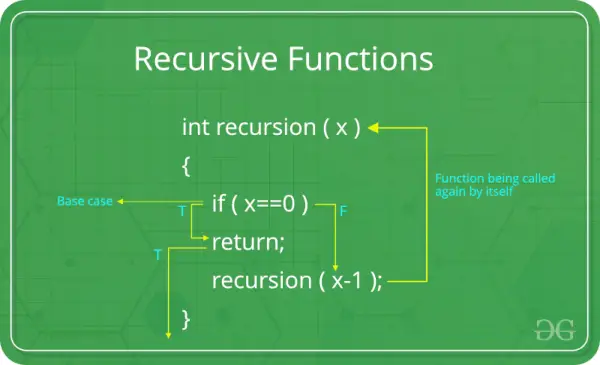
Рекурсивну функцію можна визначити як підпрограму, яка викликає сама себе прямо чи опосередковано.
Іншими словами, рекурсивна функція — це функція, яка вирішує проблему шляхом розв’язання менших екземплярів тієї самої проблеми. Ця техніка зазвичай використовується в програмуванні для вирішення проблем, які можна розбити на простіші подібні підпроблеми.
Необхідність рекурсивної функції:
Рекурсивна функція — це функція, яка розв’язує задачу, розв’язуючи менші екземпляри тієї самої задачі. Ця техніка часто використовується в програмуванні для вирішення проблем, які можна розбити на простіші подібні підпроблеми.
1. Розв'язування комплексних завдань:
Рекурсивні функції розбивають складні проблеми на менші екземпляри тієї самої проблеми, що призводить до компактного та читабельного коду.
2. Розділяй і володарюй:
Рекурсивні функції підходять для таких алгоритмів «розділяй і володарюй», як сортування злиттям і швидке сортування, поділ проблем на менші підпроблеми, їх рекурсивне розв’язання та об’єднання рішень із вихідною проблемою.
3. Відстеження назад :
Рекурсивне відстеження ідеально підходить для дослідження та вирішення таких проблем, як N-Queens і Sudoku.
4. Динамічний програмування:
Рекурсивні функції ефективно вирішують задачі динамічного програмування, розв’язуючи підпроблеми та об’єднуючи їх рішення в повне рішення.
5. Дерево і структури графів:
Рекурсивні функції чудово підходять для роботи з деревоподібними та графовими структурами, спрощуючи завдання обходу та розпізнавання шаблонів .
Як написати рекурсивну функцію:
Компоненти рекурсивної функції:
Базовий випадок: Кожна рекурсивна функція повинна мати базовий випадок. Базовий варіант — це найпростіший сценарій, який не потребує подальшої рекурсії. Це умова завершення, яка запобігає нескінченному виклику самої себе функції. Без належного базового випадку рекурсивна функція може призвести до нескінченної рекурсії.
Рекурсивний випадок: У рекурсивному випадку функція викликає сама себе зі зміненими аргументами. Це суть рекурсії – вирішення більшої проблеми шляхом її розбиття на менші екземпляри тієї самої проблеми. Рекурсивний випадок має наближатися до базового з кожною ітерацією.
Розглянемо на прикладі факторіал числа :
У цьому прикладі основний випадок - коли п є 0 , і функція повертає 1 . Рекурсивний відмінок множиться п з результатом функції, викликаної з параметром n – 1 . Процес триває, доки не буде досягнуто базового варіанту.
Важливо переконатися, що рекурсивна функція має правильний базовий випадок і що рекурсивні виклики ведуть до базового випадку, інакше процедура може працювати нескінченно, що призведе до переповнення стека (перевищення доступної пам’яті, виділеної для викликів функцій).
Нижче наведено реалізацію факториала числа:
C++ #include using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * factorial(n - 1); } // Driver Code int main() { int n = 4; cout << 'Factorial of ' << n << ' is:' << factorial(n); return 0; }> Java import java.util.Scanner; public class Factorial { // Recursive Function to calculate the factorial of a number static int factorial(int n) { // Base case: If n is 0, the factorial is 1. if (n == 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } public static void main(String[] args) { int n = 4; // Calculate and print the factorial of n. int result = factorial(n); System.out.println('Factorial of ' + n + ' is: ' + result); } }> Python # Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))> C# using System; class Program { // Recursive Function to calculate Factorial of a number static int Factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * Factorial(n - 1); } // Driver Code static void Main() { int n = 4; Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n)); } }> Javascript // Function to calculate the factorial of a number using recursion function factorial(n) { // Base case: If n is 0, the factorial is 1. if (n === 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } // Main function function main() { // Given number let n = 4; // Calculate the factorial of n. let result = factorial(n); // Print the result console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();> Вихід
Factorial of 4 is:24>
Часова складність: O(n)
Допоміжний простір: O(n)
