Квадрант визначається як область у просторі, яка розділена на чотири рівні частини двома осями, а саме віссю X і віссю Y у декартовій площині. Ці дві осі перетинаються під кутом 90 градусів, і чотири утворені таким чином області називаються чотирма квадрантами, а саме I квадрант, II квадрант, III квадрант і IV квадрант.
unix проти windows
У цій статті ми розглянемо основні поняття квадранта, зокрема, що таке квадрант, його площа, графік квадранта, декартова площина, умовні знаки в квадранті, абсциса та координата, а також нанесення точок на квадрант.
Зміст
- Що таке квадранти графіка?
- Конвенція знаків у квадрантах
- Нанесення точок на квадранти
- Тригонометричні значення в різних квадрантах
Що таке квадранти графіка?
Квадрант — це визначена область на a Декартова площина , створений перетином осей X і Y. У цій площині утворюються чотири квадранти, кожен зі своїми унікальними рисами. Перший квадрант у верхньому правому куті має позитивні координати x і y. Другий квадрант, у верхньому лівому куті, має негативні координати x і позитивні координати y тощо. Розуміння цих квадрантів має важливе значення для визначення та інтерпретації точок на графіку, що забезпечує систематичний спосіб навігації та аналізу декартових координат.
4 квадранти на координатній площині
Декартова площина, утворена осями X і Y, розділена на чотири квадранти, кожен з яких має різні характеристики:
- Перший квадрант: Координати x і y, розташовані у верхньому правому куті, додатні. Цей квадрант представляє точки у верхній правій частині площини.
- Другий квадрант: Розташована у верхньому лівому куті, координата x є від’ємною, а координата y – додатною. Цей квадрант охоплює точки у верхній лівій частині площини.
- Третій квадрант: Розташовані в нижньому лівому куті, обидві координати x і y є від’ємними. Точки в нижній лівій частині площини потрапляють у цей квадрант.
- Четвертий квадрант: У нижньому правому куті координата x додатна, а координата y від’ємна. Цей квадрант містить точки в нижній правій частині площини.
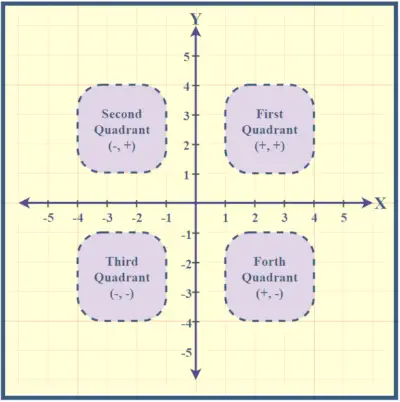
Квадранти нумеруються проти годинникової стрілки, починаючи з правого верхнього кута. Точка, де перетинаються осі X і Y, називається початком координат з координатами (0,0), що вказують нульові значення як для x, так і для y. Розуміння цих квадрантів допомагає знаходити точки в декартовій площині.
Що таке походження?
Початкова точка на графіку, відома як початок координат і показана як (0, 0), є місцем перетину горизонтальної осі x і вертикальної осі y. Це означає, що в початку координат значення x і y дорівнюють нулю. Він служить точкою відліку для визначення місцезнаходження інших точок на графіку. На зображенні, доданому вище, точка O показує початок координат.
Абсциса і ордината в квадрантах
У чотирьох квадрантах числа представлені парами (a, b), де «a» позначає координату x, а «b» — координату y. Щоб визначити, де знаходиться точка, не будуючи графіка, зверніть увагу на знаки координати x (абсциса) і координати y (ордината). Наприклад, якщо у вас є така точка, як Q (3, -5), знаки (+ve, -ve) вказують, що вона знаходиться в квадранті IV.
Абсциса показує горизонтальну відстань від осі Y. Позитивна абсциса означає праворуч, а в нашому прикладі абсциса = 3 означає перехід праворуч від початку координат уздовж осі х на 3 одиниці.
Ордината вказує відстань по вертикалі від початку координат. Від’ємна ордината означає опускання від початку координат уздовж осі y. У прикладі ордината = -5 означає зменшення на 5 одиниць.
Конвенція знаків у квадрантах
Позначення знаків у квадрантах можна легко зрозуміти, використовуючи зображення, додане нижче,

У площині XY, коли ми рухаємося зліва направо вздовж осі x, координата x збільшується. Подібним чином уздовж осі y переміщення знизу вгору призводить до збільшення координати y. Площина XY поділена на чотири квадранти, кожен з яких має певні умовні знаки для координат x і y:
| Квадрант | х-координата | y-координата |
|---|---|---|
| 1-й квадрант | Позитивний (+) | Позитивний (+) |
| 2-й квадрант | негативний (-) | Позитивний (+) |
| 3-й квадрант | негативний (-) | негативний (-) |
| 4-й квадрант | Позитивний (+) | негативний (-) |
Отже, точки в 1-му квадранті мають додатні значення як для x, так і для y, точки в 2-му квадранті мають від’ємне значення x і додатне значення y, 3-й квадрант має як від’ємні значення x, так і y, а 4-й квадрант має додатне значення x і негативне y.
Нанесення точок на квадранти
У декартовій площині точки позначаються віссю x і y. Ці точки позначаються як (a, b), де «a» — координата x (абсциса), а «b» — координата y (ордината). Щоб розмістити точку в квадранті, враховуємо знаки цих координат. Значення x і y представляють, наскільки далеко точка знаходиться від осі x і y відповідно.
Наприклад, нанесіть точку (2, -5) на декартову площину. Аналізуючи знак координат, виявляється, що точка знаходиться в 4-му квадранті. Це буде 2 одиниці від осі x (праворуч) і 5 одиниць від осі y (вниз), використовуючи початок координат як точку відліку.
Тригонометричні значення в різних квадрантах
Значення різноманітні тригонометричні функції у різних квадрантах можна дізнатися, вивчивши таблицю, додану нижче,
| Квадрант | без | Cos | Так | Косеканс | Січна | Котангенс |
|---|---|---|---|---|---|---|
| 1-й квадрант | + | + | + | + | + | + |
| 2-й квадрант | + | – | + | + | – | – Логіка 1-го порядку |
| 3-й квадрант | – | – | – | – | – | + |
| 4-й квадрант | – | – | – | – | + | – |
У 1-му квадранті всі тригонометричні співвідношення додатні. У 2-му квадранті синус і косеканс додатні (+), а косинус і секанс від’ємні (-). У 3-му квадранті тангенс і котангенс додатні (+), а косинус і секанс від’ємні (-). У 4-му квадранті синус і косеканс від'ємні (-), а косинус і секанс додатні (+).
Детальніше,
- Координатна геометрія
- Паралельні прямі
- Формула відстані
Розв’язані приклади на квадранті
Приклад 1: Накресліть точку A (3, -4) і визначте її квадрант.
рішення:
Точка А знаходиться в координатах (3, -4). Оскільки координата x додатна (3), а координата y від’ємна (-4), точка A лежить у квадранті IV.
Приклад 2: Накресліть точку P (-5, 2) і визначте її квадрант
рішення:
Координати точки P дорівнюють (-5, 2). Щоб визначити квадрант, досліджуємо знаки координат x і y.
Координата X дорівнює -5, що вказує на положення ліворуч від початку координат.
Координата Y дорівнює 2, що вказує на положення над початком координат.
Отже, оскільки координата x від'ємна, а координата y додатна, точка P знаходиться в квадранті II.
еталонна модель osi в мережахТочка P (-5, 2) розташована в квадранті II декартової площини.
Практичні задачі на квадрантах
Проблема 1: Нанесіть точку (1, -1) і визначте її квадрант.
Проблема 2: Знайдіть три точки на осі х і визначте їх квадранти.
Проблема 3: Якщо точка лежить на осі y з координатами (0, -3), у якому квадранті вона знаходиться?
Проблема 4: Знайдіть точки Q (2, 2), R (-2, -2) і S (0, 0) і перевірте колінеарність.
Проблема 5: Нанесіть точку (-4, -3) і поясніть, у якому квадранті вона знаходиться.
Поширені запитання щодо Quadrants
1. Що таке квадрант у математиці?
У математиці квадрант — це одна з чотирьох секцій, утворених перетином двох перпендикулярних прямих або осей. Ці осі зазвичай позначаються як вісь x і вісь y у декартовій системі координат.
2. Як називається перетин двох осей?
Точка перетину двох осей декартової системи координат називається початком координат. Він представлений точкою, де зустрічаються вісь x і вісь y, зазвичай позначається як (0,0).
3. Що таке 4 квадранти?
Чотири квадранти - це перерізи, утворені поділом декартової координатної площини на чотири рівні частини. Вони позначаються як перший квадрант (Q1), другий квадрант (Q2), третій квадрант (Q3) і четвертий квадрант (Q4).
4. Який квадрант додатний?
Додатним квадрантом у декартовій системі координат є перший квадрант (Q1). У цьому квадранті координати x і y додатні.
5. Яке використання квадрантів у графіках?
Квадранти на графіках забезпечують систематичний спосіб організації та розташування точок на основі їхніх координат. Вони допомагають візуалізувати зв’язки між змінними та аналізувати закономірності в наборах даних, полегшуючи інтерпретацію графічних зображень.
6. Який квадрант має обидва значення додатних координат?
Перший квадрант (Q1) – це квадрант, де координати точок x і y додатні. Це єдиний квадрант з обома позитивними значеннями.
7. Що таке 4 квадранти кола?
Концепція квадрантів не застосовується безпосередньо до кіл. Натомість кола поділено на кути, виміряні в градусах. Однак, якщо йдеться про кругові сектори, можна використовувати такі терміни, як перший сектор, другий сектор, третій сектор і четвертий сектор, що відповідають різним кутовим областям.
