 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; }За даним бінарним деревом знайдіть довжину найдовшого шляху, який складається з вузлів із послідовними значеннями в порядку зростання. Кожен вузол розглядається як шлях довжиною 1.
приклади:
In below diagram binary tree with longest consecutive path(LCP) are shown :
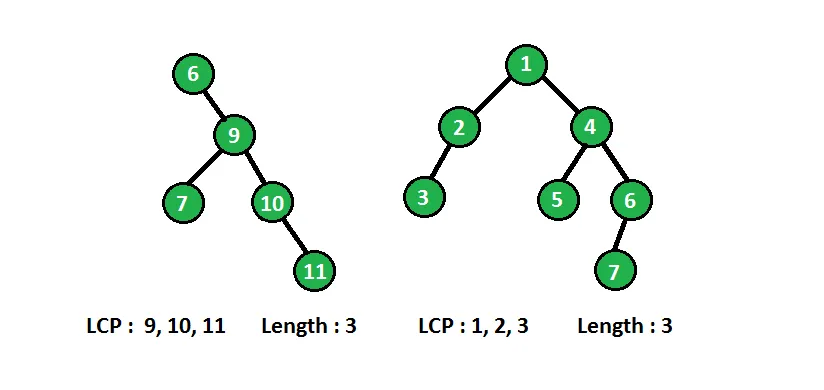
Ми можемо вирішити вищезазначену задачу рекурсивно. На кожному вузлі нам потрібна інформація про його батьківський вузол, якщо поточний вузол має значення на один більше, ніж його батьківський вузол, тоді він робить послідовний шлях на кожному вузлі, ми порівняємо значення вузла з його батьківським значенням і відповідно оновимо найдовший послідовний шлях.
Щоб отримати значення батьківського вузла, ми передамо (node_value + 1) як аргумент рекурсивного методу та порівняємо значення вузла з цим значенням аргументу, якщо воно задовольняє, оновимо поточну довжину послідовного шляху, інакше повторно ініціалізуємо поточну довжину шляху на 1.
Перегляньте код нижче для кращого розуміння:
C++// C/C++ program to find longest consecutive // sequence in binary tree #include
// Java program to find longest consecutive // sequence in binary tree class Node { int data; Node left right; Node(int item) { data = item; left = right = null; } } class Result { int res = 0; } class BinaryTree { Node root; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive(Node root) { if (root == null) return 0; Result res = new Result(); // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res.res; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil(Node root int curlength int expected Result res) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res.res = Math.max(res.res curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = new Node(6); tree.root.right = new Node(9); tree.root.right.left = new Node(7); tree.root.right.right = new Node(10); tree.root.right.right.right = new Node(11); System.out.println(tree.longestConsecutive(tree.root)); } } // This code is contributed by shubham96301
# Python3 program to find longest consecutive # sequence in binary tree # A utility class to create a node class newNode: def __init__(self data): self.data = data self.left = self.right = None # Utility method to return length of # longest consecutive sequence of tree def longestConsecutiveUtil(root curLength expected res): if (root == None): return # if root data has one more than its # parent then increase current length if (root.data == expected): curLength += 1 else: curLength = 1 # update the maximum by current length res[0] = max(res[0] curLength) # recursively call left and right subtree # with expected value 1 more than root data longestConsecutiveUtil(root.left curLength root.data + 1 res) longestConsecutiveUtil(root.right curLength root.data + 1 res) # method returns length of longest consecutive # sequence rooted at node root def longestConsecutive(root): if (root == None): return 0 res = [0] # call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res) return res[0] # Driver Code if __name__ == '__main__': root = newNode(6) root.right = newNode(9) root.right.left = newNode(7) root.right.right = newNode(10) root.right.right.right = newNode(11) print(longestConsecutive(root)) # This code is contributed by PranchalK
// C# program to find longest consecutive // sequence in binary tree using System; class Node { public int data; public Node left right; public Node(int item) { data = item; left = right = null; } } class Result { public int res = 0; } class GFG { Node root; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive(Node root) { if (root == null) return 0; Result res = new Result(); // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res.res; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil(Node root int curlength int expected Result res) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res.res = Math.Max(res.res curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code public static void Main(String []args) { GFG tree = new GFG(); tree.root = new Node(6); tree.root.right = new Node(9); tree.root.right.left = new Node(7); tree.root.right.right = new Node(10); tree.root.right.right.right = new Node(11); Console.WriteLine(tree.longestConsecutive(tree.root)); } } // This code is contributed by 29AjayKumar
<script> // JavaScript program to find longest consecutive // sequence in binary tree class Node { constructor(item) { this.data=item; this.left = this.right = null; } } let res = 0; let root; function longestConsecutive(root) { if (root == null) return 0; res=[0]; // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res[0]; } // Utility method to return length of longest // consecutive sequence of tree function longestConsecutiveUtil(rootcurlength expectedres) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res[0] = Math.max(res[0] curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code root = new Node(6); root.right = new Node(9); root.right.left = new Node(7); root.right.right = new Node(10); root.right.right.right = new Node(11); document.write(longestConsecutive(root)); // This code is contributed by rag2127 </script>
Вихід
3
Часова складність: O(N), де N – кількість вузлів у даному бінарному дереві.
Допоміжний простір: O(log(N))
Також обговорено за посиланням нижче:
Максимальна послідовне збільшення довжини шляху у двійковому дереві
