Ми бачили різні методи з різними часовими складностями для обчислення LCA в n-арному дереві:-
Спосіб 1: Наївний метод (обчислення шляху від кореня до вузла) | O(n) на запит
Спосіб 2: Використання декомпозиції Sqrt | O(sqrt H)
Спосіб 3: Використання підходу розрідженої матриці DP | O (вхід)
Давайте вивчимо інший метод, який має швидший час запиту, ніж усі вищезгадані методи. Тому нашою метою буде розрахувати LCA в постійний час ~ O(1) . Давайте подивимося, як ми можемо цього досягти.
Спосіб 4: Використання запиту на мінімальний діапазон
Ми обговорили LCA та RMQ для бінарного дерева . Тут ми обговорюємо перетворення проблеми LCA в задачу RMQ для n-арного дерева.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Ключова концепція: У цьому методі ми зменшимо нашу проблему LCA до проблеми RMQ (запит мінімального діапазону) над статичним масивом. Коли ми це зробимо, ми зв’яжемо запити щодо мінімального діапазону з необхідними запитами LCA.
Першим кроком буде розкладання дерева на плоский лінійний масив. Для цього ми можемо застосувати блукання Ейлера. Прогулянка Ейлера дасть попередній обхід графа. Отже, ми виконаємо обхід Ейлера по дереву та збережемо вузли в масиві, коли ми їх відвідаємо. Цей процес зменшує дерево > 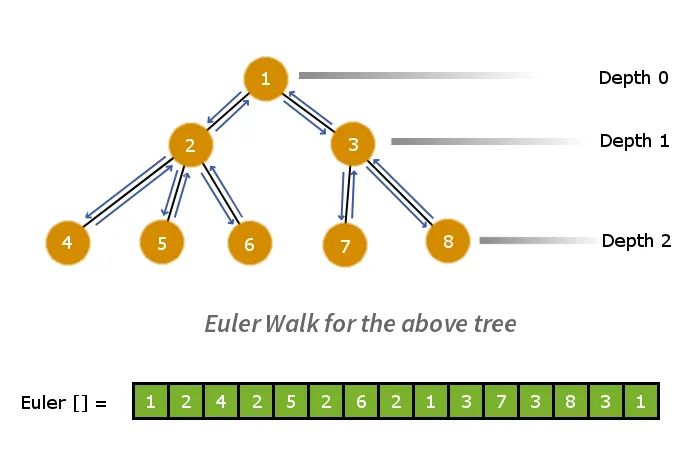
Тепер давайте подумаємо в загальних рисах: розглянемо будь-які два вузли на дереві. Буде точно один шлях, що з’єднує обидва вузли, і вузол, який має найменше значення глибини на шляху, буде LCA двох заданих вузлів.
Тепер візьмемо будь-які два різні вузли в і v в масиві блукань Ейлера. Тепер усі елементи на шляху від u до v будуть лежати між індексами вузлів u і v у масиві обходу Ейлера. Тому нам просто потрібно обчислити вузол із мінімальною глибиною між індексом вузла u та вузла v у масиві Ейлера.
Для цього ми підтримуватимемо інший масив, який міститиме глибину всіх вузлів, що відповідає їхній позиції в масиві блукання Ейлера, щоб ми могли застосувати до нього наш алгоритм RMQ.
Нижче наведено масив Ейлера, паралельний його масиву глибинних доріжок.

одиночний дизайн
Приклад: - Розглянемо два вузли вузол 6 і вузол 7 в масиві Ейлера. Щоб обчислити LCA вузла 6 і вузла 7, ми шукаємо найменше значення глибини для всіх вузлів між вузлом 6 і вузлом 7.
тому вузол 1 має найменший значення глибини = 0 і, отже, це LCA для вузла 6 і вузла 7.

Реалізація: -
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
Шлях Ейлера та масив глибини такі ж, як описано вище
метод java
Індекс першого вигляду FAI[] : Масив індексів першого вигляду зберігатиме індекс для першої позиції кожного вузла в масиві шляху Ейлера. FAI[i] = перша поява i-го вузла в масиві Ейлера.
Реалізація вищевказаного методу наведена нижче:
Реалізація:
C++// C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std; #define sz 101 vector < int > adj[sz]; // stores the tree vector < int > euler; // tracks the eulerwalk vector < int > depthArr; // depth for each node corresponding // to eulerwalk int FAI[sz]; // stores first appearance index of every node int level[sz]; // stores depth for all nodes in the tree int ptr; // pointer to euler walk int dp[sz][18]; // sparse table int logn[sz]; // stores log values int p2[20]; // stores power of 2 void buildSparseTable(int n) { // initializing sparse table memset(dp-1sizeof(dp)); // filling base case values for (int i=1; i<n; i++) dp[i-1][0] = (depthArr[i]>depthArr[i-1])?i-1:i; // dp to fill sparse table for (int l=1; l<15; l++) for (int i=0; i<n; i++) if (dp[i][l-1]!=-1 and dp[i+p2[l-1]][l-1]!=-1) dp[i][l] = (depthArr[dp[i][l-1]]>depthArr[dp[i+p2[l-1]][l-1]])? dp[i+p2[l-1]][l-1] : dp[i][l-1]; else break; } int query(int lint r) { int d = r-l; int dx = logn[d]; if (l==r) return l; if (depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]) return dp[r-p2[dx]][dx]; else return dp[l][dx]; } void preprocess() { // memorizing powers of 2 p2[0] = 1; for (int i=1; i<18; i++) p2[i] = p2[i-1]*2; // memorizing all log(n) values int val = 1ptr=0; for (int i=1; i<sz; i++) { logn[i] = ptr-1; if (val==i) { val*=2; logn[i] = ptr; ptr++; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs(int curint prevint dep) { // marking FAI for cur node if (FAI[cur]==-1) FAI[cur] = ptr; level[cur] = dep; // pushing root to euler walk euler.push_back(cur); // incrementing euler walk pointer ptr++; for (auto x:adj[cur]) { if (x != prev) { dfs(xcurdep+1); // pushing cur again in backtrack // of euler walk euler.push_back(cur); // increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr() { for (auto x : euler) depthArr.push_back(level[x]); } int LCA(int uint v) { // trivial case if (u==v) return u; if (FAI[u] > FAI[v]) swap(uv); // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } void addEdge(int uint v) { adj[u].push_back(v); adj[v].push_back(u); } int main(int argc char const *argv[]) { // constructing the described tree int numberOfNodes = 8; addEdge(12); addEdge(13); addEdge(24); addEdge(25); addEdge(26); addEdge(37); addEdge(38); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; memset(FAI-1sizeof(FAI)); dfs(100); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.size()); cout << 'LCA(67) : ' << LCA(67) << 'n'; cout << 'LCA(64) : ' << LCA(64) << 'n'; return 0; }
// Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList; import java.util.Arrays; class GFG{ static int sz = 101; @SuppressWarnings('unchecked') // Stores the tree static ArrayList<Integer>[] adj = new ArrayList[sz]; // Tracks the eulerwalk static ArrayList<Integer> euler = new ArrayList<>(); // Depth for each node corresponding static ArrayList<Integer> depthArr = new ArrayList<>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[][] dp = new int[sz][18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[i][j] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 1][0] = (depthArr.get(i) > depthArr.get(i - 1)) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[i][l - 1] != -1 && dp[i + p2[l - 1]][l - 1] != -1) dp[i][l] = (depthArr.get(dp[i][l - 1]) > depthArr.get( dp[i + p2[l - 1]][l - 1])) ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr.get(dp[l][dx]) > depthArr.get(dp[r - p2[dx]][dx])) return dp[r - p2[dx]][dx]; else return dp[l][dx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.add(cur); // Incrementing euler walk pointer ptr++; for(Integer x : adj[cur]) { if (x != prev) { dfs(x cur dep + 1); // Pushing cur again in backtrack // of euler walk euler.add(cur); // Increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { for(Integer x : euler) depthArr.add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler.get(query(FAI[u] FAI[v])); } static void addEdge(int u int v) { adj[u].add(v); adj[v].add(u); } // Driver code public static void main(String[] args) { for(int i = 0; i < sz; i++) { adj[i] = new ArrayList<>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Arrays.fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.size()); System.out.println('LCA(67) : ' + LCA(6 7)); System.out.println('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by sanjeev2552
# Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range(101)] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [-1] * 101 # stores depth for all nodes in the tree level = [0] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[-1] * 18 for _ in range(101)] # stores log values logn = [0] * 101 # stores power of 2 p2 = [0] * 20 def buildSparseTable(n: int): # initializing sparse table for i in range(n): dp[i][0] = i-1 if depthArr[i] > depthArr[i-1] else i # dp to fill sparse table for l in range(1 15): for i in range(n): if dp[i][l-1] != -1 and dp[i+p2[l-1]][l-1] != -1: dp[i][l] = dp[i+p2[l-1]][l-1] if depthArr[dp[i][l-1] ] > depthArr[dp[i+p2[l-1]][l-1]] else dp[i][l-1] else: break def query(l: int r: int) -> int: d = r-l dx = logn[d] if l == r: return l if depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]: return dp[r-p2[dx]][dx] else: return dp[l][dx] def preprocess(): global ptr # memorizing powers of 2 p2[0] = 1 for i in range(1 18): p2[i] = p2[i-1]*2 # memorizing all log(n) values val = 1 ptr = 0 for i in range(1 101): logn[i] = ptr-1 if val == i: val *= 2 logn[i] = ptr ptr += 1 def dfs(cur: int prev: int dep: int): global ptr # marking FAI for cur node if FAI[cur] == -1: FAI[cur] = ptr level[cur] = dep # pushing root to euler walk euler.append(cur) # incrementing euler walk pointer ptr += 1 for x in adj[cur]: if x != prev: dfs(x cur dep+1) # pushing cur again in backtrack # of euler walk euler.append(cur) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr(): global depthArr for x in euler: depthArr.append(level[x]) def LCA(u: int v: int) -> int: # trivial case if u == v: return u if FAI[u] > FAI[v]: u v = v u # doing RMQ in the required range return euler[query(FAI[u] FAI[v])] def addEdge(u v): adj[u].append(v) adj[v].append(u) # constructing the described tree numberOfNodes = 8 addEdge(1 2) addEdge(1 3) addEdge(2 4) addEdge(2 5) addEdge(2 6) addEdge(3 7) addEdge(3 8) # performing required precalculations preprocess() # doing the Euler walk ptr = 0 FAI = [-1] * (numberOfNodes + 1) dfs(1 0 0) # creating depthArray corresponding to euler[] makeArr() # building sparse table buildSparseTable(len(depthArr)) print('LCA(67) : ' LCA(6 7)) print('LCA(64) : ' LCA(6 4))
// C# program to demonstrate LCA of n-ary // tree in constant time. using System; using System.Collections.Generic; public class GFG { static int sz = 101; // Stores the tree static List<int>[] adj = new List<int>[sz]; // Tracks the eulerwalk static List<int> euler = new List<int>(); // Depth for each node corresponding static List<int> depthArr = new List<int>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[] dp = new int[sz 18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[ij] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 10] = (depthArr[i] > depthArr[i - 1]) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[il - 1] != -1 && dp[i + p2[l - 1]l - 1] != -1) dp[il] = (depthArr[dp[il - 1]] > depthArr[dp[i + p2[l - 1]l - 1]]) ? dp[i + p2[l - 1]l - 1] : dp[il - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr[dp[ldx]] > depthArr[dp[r - p2[dx]dx]]) return dp[r - p2[dx]dx]; else return dp[ldx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.Add(cur); // Incrementing euler walk pointer ptr++; foreach (int x in adj[cur]) { if (x != prev) { dfs(x cur dep + 1); euler.Add(cur); ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { foreach (int x in euler) depthArr.Add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } static void addEdge(int u int v) { adj[u].Add(v); adj[v].Add(u); } // Driver Code static void Main(string[] args) { int sz = 9; adj = new List<int>[sz]; for (int i = 0; i < sz; i++) { adj[i] = new List<int>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Array.Fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.Count); Console.WriteLine('LCA(67) : ' + LCA(6 7)); Console.WriteLine('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by Prince Kumar
let adj = []; for (let _ = 0; _ < 101; _++) { adj.push([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array(101).fill(-1); // stores depth for all nodes in the tree let level = new Array(101).fill(0); // pointer to euler walk let ptr = 0; // sparse table let dp = []; for (let _ = 0; _ < 101; _++) { dp.push(new Array(18).fill(-1)); } // stores log values let logn = new Array(101).fill(0); // stores power of 2 let p2 = new Array(20).fill(0); function buildSparseTable(n) { // initializing sparse table for (let i = 0; i < n; i++) { dp[i][0] = i - 1 >= 0 && depthArr[i] > depthArr[i - 1] ? i - 1 : i; } // dp to fill sparse table for (let l = 1; l < 15; l++) { for (let i = 0; i < n; i++) { if ( dp[i][l - 1] !== -1 && dp[i + p2[l - 1]][l - 1] !== -1 ) { dp[i][l] = depthArr[dp[i][l - 1]] > depthArr[dp[i + p2[l - 1]][l - 1]] ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; } else { break; } } } } function query(l r) { let d = r - l; let dx = logn[d]; if (l === r) { return l; } if (depthArr[dp[l][dx]] > depthArr[dp[r - p2[dx]][dx]]) { return dp[r - p2[dx]][dx]; } else { return dp[l][dx]; } } function preprocess() { // memorizing powers of 2 p2[0] = 1; for (let i = 1; i < 18; i++) { p2[i] = p2[i - 1] * 2; } // memorizing all log(n) values let val = 1; ptr = 0; for (let i = 1; i < 101; i++) { logn[i] = ptr - 1; if (val === i) { val *= 2; logn[i] = ptr; ptr += 1; } } } function dfs(cur prev dep) { // marking FAI for cur node if (FAI[cur] === -1) { FAI[cur] = ptr; } level[cur] = dep; // pushing root to euler walk euler.push(cur); // incrementing euler walk pointer ptr += 1; for (let x of adj[cur]) { if (x !== prev) { dfs(x cur dep + 1); // pushing cur again in backtrack // of euler walk euler.push(cur); // increment euler walk pointer ptr += 1; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr() { for (let x of euler) { depthArr.push(level[x]); } } function LCA(u v) { // trivial case if (u === v) { return u; } if (FAI[u] > FAI[v]) { [u v] = [v u]; } // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } function addEdge(u v) { adj[u].push(v); adj[v].push(u); } // constructing the described tree let numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; FAI = new Array(numberOfNodes + 1).fill(-1); dfs(1 0 0); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.length); console.log('LCA(67) : ' LCA(6 7)); console.log('LCA(64) : ' LCA(6 4));
Вихід
LCA(67) : 1 LCA(64) : 2
Примітка: Ми попередньо розраховуємо всю необхідну потужність двійок, а також попередньо обчислюємо всі необхідні значення журналу, щоб забезпечити постійну часову складність для кожного запиту. Інакше, якби ми робили обчислення журналу для кожної операції запиту, наша часова складність не була б постійною.
Часова складність: Процес перетворення з LCA на RMQ здійснюється за допомогою Euler Walk O(n) час.
Попередня обробка для розрідженої таблиці в RMQ займає O(nlogn) часу, а відповідь на кожен запит є процесом постійного часу. Тому загальна часова складність становить O(nlogn) - попередня обробка та О(1) для кожного запиту.
Допоміжний простір: O(n+s)
Створіть вікторину
