Finite Automata (FA) — найпростіша машина для розпізнавання шаблонів. Вона використовується для характеристики звичайної мови, наприклад: /baa+!/.
Він також використовується для аналізу та розпізнавання виразів природної мови. Скінченний автомат або кінцевий автомат — це абстрактна машина, яка має п’ять елементів або кортежів. Він має набір станів і правил для переходу з одного стану в інший, але це залежить від застосованого символу введення. На основі станів і набору правил вхідний рядок може бути прийнятим або відхиленим. По суті, це абстрактна модель цифрового комп’ютера, який зчитує вхідний рядок і змінює свій внутрішній стан залежно від поточного вхідного символу. Кожен автомат визначає мову, тобто набір рядків, які він приймає. На наступному малюнку показано деякі важливі особливості загальної автоматизації.
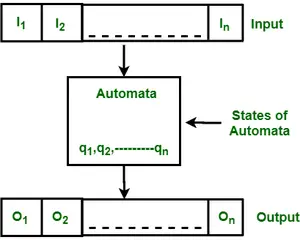
Малюнок: Особливості кінцевих автоматів
На наведеному вище малюнку показано наступні особливості автоматів:
- Введення
- Вихід
- Стани автоматів
- Державне відношення
- Вихідне відношення
Скінченний автомат складається з наступного:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Формальна специфікація машини
подвійний в java
{ Q, ?, q, F, ? }> ФА характеризується двома типами:
1) Детерміновані кінцеві автомати (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->Q.> У DFA для певного вхідного символу машина переходить лише в один стан. Функція переходу визначається для кожного стану для кожного вхідного символу. Також у DFA нульове (або?) переміщення заборонено, тобто DFA не може змінити стан без будь-якого введеного символу.
хакерська обробка
Наприклад, створіть DFA, який приймає мову з усіма рядками, що закінчуються на «a».
Дано: ? = {a,b}, q = {q0}, F={q1}, Q = {q0, q1}
Спочатку розглянемо мовний набір усіх можливих прийнятних рядків, щоб побудувати точну діаграму переходу станів.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, батько, батько, батько, батько}
Вище наведена проста підмножина можливих прийнятних рядків, тут може бути багато інших рядків, які закінчуються на «a» і містять символи {a,b}.
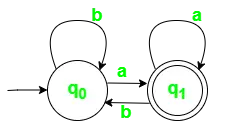
Рис. 1. Діаграма переходу стану для DFA з ? = {a, b}
Рядки не приймаються,
ab, bb, aab, abbb тощо.
Таблиця переходів станів для вищезгаданого автомата,
| ?Державасимвол? | a | b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q0 |
Важливо зауважити, що може бути багато можливих DFA для шаблону . Як правило, бажано використовувати DFA з мінімальною кількістю станів.
2) Недетерміновані кінцеві автомати (NFA): NFA схожий на DFA, за винятком наступних додаткових функцій:
- Нульове (чи?) переміщення дозволено, тобто він може рухатися вперед без читання символів.
- Можливість передачі в будь-яку кількість станів для певного входу.
Однак наведені вище функції не додають жодної потужності NFA. Якщо ми порівняємо обидва з точки зору потужності, обидва еквівалентні.
перетворити рядок на enum
Завдяки наведеним вище додатковим функціям NFA має іншу функцію переходу, решта те саме, що й DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Q.>
Як ви можете бачити у функції переходу для будь-якого вхідного значення, включаючи null (або?), NFA може переходити до будь-якої кількості станів. Наприклад, нижче наведено NFA для описаної вище проблеми.
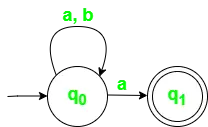
Рис. 2. Діаграма переходу стану для NFA з ? = {a, b}
Таблиця переходів станів для вищезгаданого автомата,
| ?Державасимвол? | a | b |
|---|---|---|
| q0 | {q0,q1} | q0 |
| q1 | ? | ? |
Важливо зауважити, що у NFA, якщо будь-який шлях для вхідного рядка веде до кінцевого стану, то вхідний рядок є прийнято . Наприклад, у наведеному вище NFA існує кілька шляхів для вхідного рядка 00. Оскільки один із шляхів веде до кінцевого стану, 00 приймається вищенаведеним NFA.
Деякі важливі моменти:
- Обґрунтування:
In case of DFA ? : Q X ? -->Q У випадку NFA? : Q X ? --> 2Q>
Тепер, якщо ви поспостерігаєте, ви дізнаєтесь Q X ? –> Q є частиною Q X ? –> 2Q.
перевертання рядка в java
З правого боку Q є підмножиною 2Qщо вказує на те, що Q міститься в 2Qабо Q є частиною 2Q, однак зворотне не вірно. Отже, математично ми можемо це зробити кожен DFA є NFA, але не навпаки . Проте є спосіб перетворити NFA на DFA, отже існує еквівалентний DFA для кожного NFA .
- І NFA, і DFA мають однакову силу, і кожен NFA можна перевести в DFA.
- У DFA і NFA може бути кілька кінцевих станів.
- NFA – це більше теоретична концепція.
- DFA використовується в лексичному аналізі в компіляторі.
- Якщо кількість станів у NFA дорівнює N, тоді його DFA може мати максимум 2Нкількість держав.
Перегляньте Тест про регулярні вирази та кінцеві автомати.
