А Спрямований ациклічний граф , часто скорочено як ДЕНЬ , є фундаментальним поняттям у теорії графів. DAG використовуються, щоб чітко та організовано показати, як речі пов’язані або залежать одне від одного. У цій статті ми дізнаємося про Спрямований ациклічний граф , його властивості та застосування в реальному житті.

Спрямований ациклічний граф

Що таке орієнтований ациклічний граф?

А Спрямований ациклічний граф (DAG) — орієнтований граф, який не містить циклів.

Наведений нижче графік представляє спрямований ациклічний граф (DAG):

Прямий ациклічний граф

Значення орієнтованого ациклічного графа:

Спрямований ациклічний граф має дві важливі особливості:

• Спрямований край s:У спрямованому ациклічному графі кожне ребро має напрямок, тобто воно йде від однієї вершини (вузла) до іншої. Цей напрямок означає a односторонній зв'язок або залежність між вузлами.
• Ациклічні: Термін ациклічні вказує, що в графі немає циклів або замкнутих циклів. Іншими словами, ви не можете пройти через послідовність спрямованих ребер і повернутися до того самого вузла, дотримуючись напрямків ребер. Утворення циклів заборонено в ДЕНЬ. Тому ця характеристика є важливою.

Спрямований ациклічний граф

Властивості орієнтованого ациклічного графа DAG:

Спрямований ациклічний граф (DAG) має різні властивості, завдяки яким їх можна використовувати в графових задачах.

Існують наступні властивості спрямованого ациклічного графа (DAG):

• Відношення досяжності: У DAG ми можемо визначити, чи існує відношення досяжності між двома вузлами. Кажуть, що вузол A доступний із вузла B, якщо існує спрямований шлях, який починається у вузлі B і закінчується у вузлі A. Це означає, що ви можете слідувати напрямку ребер у графі, щоб дістатися від B до A.
• Перехідне закриття: Транзитивне замикання орієнтованого графа — це новий граф, який представляє всі прямі та непрямі зв’язки або зв’язки між вузлами вихідного графа. Іншими словами, він повідомляє вам, до яких вузлів можна дістатися з інших вузлів, дотримуючись одного або кількох спрямованих ребер.

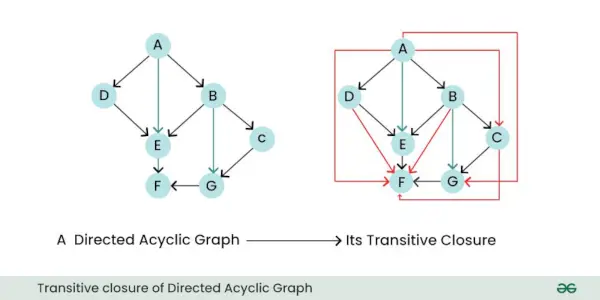
Транзитивне замикання орієнтованого ациклічного графа

• Транзитивне скорочення: Транзитивне скорочення орієнтованого графа — це новий граф, який зберігає лише істотні прямі зв’язки між вузлами, видаляючи будь-які непотрібні непрямі ребра. По суті, це спрощує граф, усуваючи ребра, які можна вивести з ребер, що залишилися.

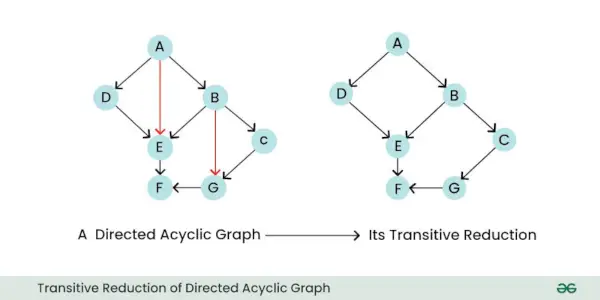
Транзитивна редукція орієнтованого ациклічного графа

• Топологічний порядок: DAG можна топологічно відсортувати, що означає, що ви можете лінійно впорядкувати його вузли таким чином, щоб для всіх ребер початковий вузол ребра відбувався раніше в послідовності. Ця властивість корисна для таких завдань, як планування та вирішення залежностей.

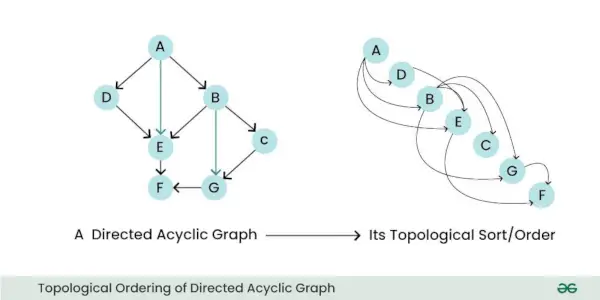
Топологічне впорядкування орієнтованого ациклічного графа

Практичне застосування DAG:

• Аналіз потоку даних: У проектуванні та оптимізації компілятора DAG використовуються для представлення потоку даних у програмі. Це допомагає оптимізувати код шляхом визначення зайвих обчислень і мертвого коду. DAG також використовуються для представлення структури базові блоки в дизайні компілятора.

• Планування завдань: DAG використовуються в управлінні проектами та плануванні завдань. Кожне завдання або завдання представлено як вузол у DAG із спрямованими ребрами, що вказують на залежності. Ациклічний характер DAG забезпечує планування завдань у логічному порядку, запобігаючи циклічній залежності.

Зважений спрямований ациклічний граф може бути використаний для представлення проблеми планування. Розглянемо приклад задачі планування завдань. Тут вершина може представляти завдання, а її вага може представляти розмір обчислення завдання. Так само ребро може представляти зв’язок між двома завданнями, а його вага може представляти вартість зв’язку:

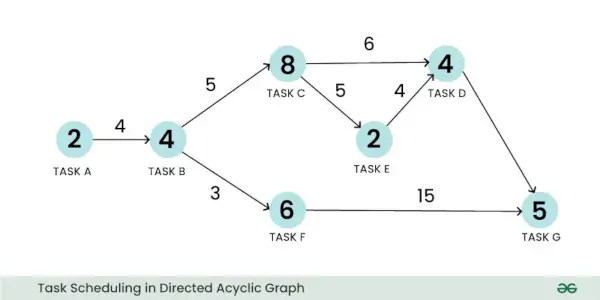
Планування завдань у спрямованому ациклічному графі

Висновок:

Таким чином, спрямовані ациклічні графи є фундаментальною концепцією теорії графів з численними практичними застосуваннями. DAG відіграють вирішальну роль у плануванні завдань, аналізі потоку даних, вирішенні залежностей і в інших сферах інформатики та техніки. Вони допомагають оптимізувати процеси, керувати залежностями та забезпечити ефективне виконання завдань або завдань.