Алгоритмічний світ прекрасний із різноманітними стратегіями та інструментами, які цілодобово розробляються для задоволення потреб у високопродуктивних обчисленнях. Насправді, коли алгоритми надихаються законами природи, спостерігаються цікаві результати. До такого класу алгоритмів належать еволюційні алгоритми. Ці алгоритми розроблені таким чином, щоб імітувати певну поведінку, а також еволюційні риси геному людини. Крім того, такий алгоритмічний дизайн не тільки обмежений людьми, але також може бути натхненний природною поведінкою певних тварин. Основна мета створення таких методологій полягає в тому, щоб забезпечити реалістичні, релевантні та водночас деякі недорогі рішення проблем, які досі не вирішувались звичайними засобами.
numpy стандартне відхилення
Таким чином, на основі таких еволюційних алгоритмів розвинулися різні методи оптимізації, що відкрило область метаевристик. Метаевристичний походить від двох грецьких слів, а саме: Мета значення на один рівень вище і heuriskein значення знайти . Такі алгоритми, як оптимізація рою частинок (PSO) і оптимізація колонії мурашок (ACO), є прикладами ройового інтелекту та метаевристики. Метою ройового інтелекту є розробка інтелектуальних багатоагентних систем, черпаючи натхнення з колективної поведінки соціальних комах, таких як мурахи, терміти, бджоли, оси та інших тваринних суспільств, таких як зграї птахів або зграї риб.
фон:
Техніка оптимізації мурашиної колонії повністю натхненна нагулювання поведінки мурашиних колоній, вперше представлений Марко Доріго в 1990-х роках. Мурахи є евсоціальними комахами, які віддають перевагу виживанню та підтримці спільноти, а не як окремі види. Вони спілкуються один з одним за допомогою звуку, дотику та феромону. Феромони це органічні хімічні сполуки, що виділяються мурахами, які викликають соціальну реакцію в представників одного виду. Це хімічні речовини, здатні діяти як гормони поза тілом особини, що виділяє секрет, впливаючи на поведінку особин, які їх приймають. Оскільки більшість мурах живе на землі, вони використовують поверхню ґрунту, щоб залишати сліди феромонів, за якими можуть стежити (відчувати запах) інші мурахи.
Мурахи живуть у громадських гніздах, і основний принцип ACO полягає в спостереженні за рухом мурах із їхніх гнізд, щоб шукати їжу найкоротшим можливим шляхом. Спочатку мурахи починають безладно пересуватися в пошуках їжі навколо своїх гнізд. Цей випадковий пошук відкриває кілька маршрутів від гнізда до джерела їжі. Тепер, виходячи з якості та кількості їжі, мурахи повертають частину їжі з необхідною концентрацією феромонів на зворотному шляху. Залежно від цих випробувань феромонів, ймовірність вибору певного шляху наступними мурахами буде керівним фактором для джерела їжі. Очевидно, ця ймовірність базується на концентрації, а також на швидкості випаровування феромону. Також можна помітити, що оскільки швидкість випаровування феромону також є вирішальним фактором, довжину кожного шляху можна легко порахувати.
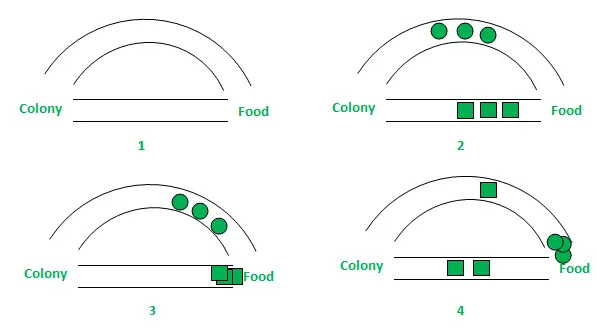
На наведеному вище малюнку для простоти розглянуто лише два можливі шляхи між джерелом їжі та гніздом мурах. Етапи можна проаналізувати таким чином:
scanner.next java
- Етап 1: усі мурахи у своєму гнізді. У середовищі відсутній вміст феромонів. (Для алгоритмічного проектування залишкова кількість феромонів може бути розглянута без впливу на ймовірність) Етап 2: Мурахи починають пошук з рівною (0,5 кожна) ймовірністю вздовж кожного шляху. Зрозуміло, що вигнутий шлях довший, а отже, час, який потрібен мурахам, щоб дістатися до джерела їжі, більше, ніж інший. Етап 3: Мурахи коротшим шляхом досягають джерела їжі раніше. Тепер, очевидно, вони стикаються з подібною дилемою відбору, але цього разу через феромонний слід уздовж більш короткого шляху, який уже доступний, ймовірність відбору вища. Етап 4: більше мурах повертається коротшим шляхом, і згодом концентрація феромонів також зростає. Крім того, через випаровування концентрація феромонів на довшому шляху зменшується, зменшуючи ймовірність вибору цього шляху на подальших етапах. Тому вся колонія поступово використовує коротший шлях із вищою ймовірністю. Отже, оптимізація шляху досягнута.
Алгоритмічний дизайн:
Що стосується описаної вище поведінки мурах, тепер можна розробити алгоритмічний дизайн. Для простоти, єдине джерело їжі та одна колонія мурашок були розглянуті лише з двома можливими шляхами проходження. Весь сценарій можна реалізувати за допомогою зважених графів, де колонія мурашок і джерело їжі діють як вершини (або вузли); шляхи служать ребрами, а значення феромонів є вагами, пов’язаними з ребрами.
Нехай графік буде G = (V, E) де V, E – ребра і вершини графа. Вершини згідно з нашим розглядом є INс (Вершина джерела – колонія мурашок) і INd (Вершина призначення – джерело їжі), два ребра є І1 і І2 з довжинами Л1 і Л2 призначені кожному. Тепер можна припустити, що відповідні значення феромонів (що вказують на їх силу). Р1 і Р2 для вершин E1і Е2відповідно. Таким чином, для кожної мурашки початкова ймовірність вибору шляху (між E1і Е2) можна виразити таким чином:
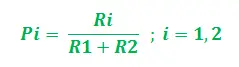
Очевидно, якщо Р1>Р2, ймовірність вибору Е1вище і навпаки. Тепер, повертаючись цим найкоротшим шляхом, скажіть Еi, значення феромону оновлюється для відповідного шляху. Оновлення виконується на основі довжини шляхів, а також швидкості випаровування феромону. Таким чином, оновлення можна поетапно реалізувати наступним чином:
- За довжиною шляху –
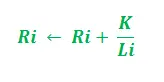
У наведеному вище оновленні i = 1, 2 і «K» служить параметром моделі. Крім того, оновлення залежить від довжини шляху. Чим коротший шлях, тим більше феромонів. Відповідно до швидкості випаровування феромону –
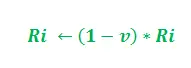
Параметр «v» належить до інтервалу (0, 1], який регулює випаровування феромонів. Далі i = 1, 2.
На кожній ітерації всі мурахи розміщуються у вихідній вершині Vс(колонія мурашок). Згодом мурахи переселяються з Vсдо Вd(джерело їжі) після кроку 1. Далі всі мурахи здійснюють свою зворотну подорож і зміцнюють свій обраний шлях на основі кроку 2.
c масив рядків
Псевдокод:
Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>
Оновлення феромонів і обчислення придатності в наведеному вище псевдокоді можна знайти за допомогою покрокових реалізацій, згаданих вище.
Таким чином, встановлено впровадження методики оптимізації ACO. Застосування ACO можна поширити на різні проблеми, такі як відомі TSP (Проблема комівояжера) .
Література:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf
