Центр вписання трикутника є точкою перетину всіх трьох бісектрис трикутника. Центр вписування є важливою точкою в трикутнику, де зустрічаються лінії, що розрізають кути навпіл. Ця точка також є центром кола, яке називається Вписане коло, яке ідеально вписується всередину трикутника та однаково дотикається до всіх трьох сторін. У цій статті розглядаються різні поняття центру вписаного трикутника, наприклад, чому ця точка важлива, як знайти її за допомогою компаса чи чисел, а також властивості центру вписаного кола.

Зміст

• Що таке центр впису трикутника?
• Властивості центру вписаного трикутника
• Формула центру вписання трикутника
• Як знайти центр вписання трикутника
• Центроїд, центр окружності, центр врізання, ортоцентр

Що таке центр впису трикутника?

Центр вписаного трикутника, як випливає з назви, є центральною точкою трикутника. Ця точка, яку ми називаємо вписаним центром, утворюється на стику, де зустрічаються всі лінії, що ділять внутрішні кути навпіл. Відстань точки від усіх трьох сторін трикутника однакова. Вписане коло трикутника також відповідає ідеальному колі всередині трикутника, і це коло називається вписаним колом трикутника.

Визначення інцентру

Центр вписаного трикутника - це точка всередині трикутника, де всі три лінії, що розрізають його внутрішні кути навпіл, сходяться разом. Ця точка знаходиться на однаковій відстані від трьох сторін трикутника, що робить її серединою трикутника. Це також центр найбільшого кола, яке може щільно поміститися всередині трикутника, який ми називаємо вписаним колом. Для символізації центру вписання ми зазвичай використовуємо літеру I,

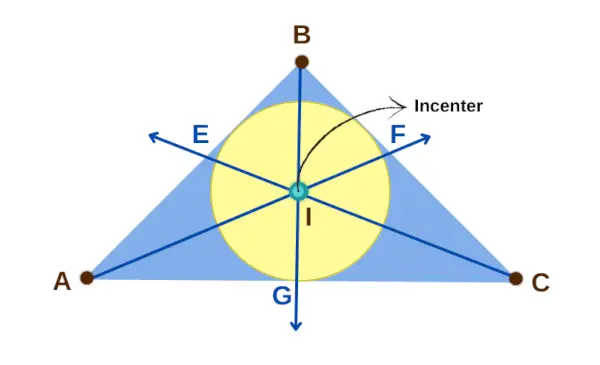
Центр вписання трикутника

Властивості центру вписаного трикутника

Деякі важливі властивості центру вписаного трикутника наведено нижче:

Властивість 1: Якщо я є центром вписаного трикутника ABC, то три пари відрізків рівні за довжиною: AE і AG, CG і CF, BF і BE. Це означає, що AE = AG, CG = CF і BF = BE.

Властивість 2: Інцентр я також має особливий зв'язок з кутами трикутника. Це призводить до того, що кути ∠BAI і ∠CAI рівні, ∠BCI і ∠ACI рівні, а ∠ABI і ∠CBI рівні. Це випливає з теореми про бісектрису кута.

Властивість 3: Інцентр я є центром кола, яке торкається всіх трьох сторін трикутника, і відстані від я до сторін трикутника (EI, FI, GI) всі однакові. Ці відстані називають внутрішніми радіусами, або радіусами вписаного кола.

Властивість 4: Ви можете обчислити площу трикутника, використовуючи півпериметр (s) і внутрішній радіус (r). Формула: A = sr, де A — площа, s — півпериметр (s = (a + b + c)/2, де a, b і c — довжини сторін трикутника), а r — в радіусі.

Властивість 5: Центр вписаного трикутника завжди залишається всередині трикутника. На відміну від ортоцентра, який у деяких випадках може бути за межами трикутника, центр вписаного завжди міститься в межах трикутника.

Формула центру вписання трикутника

Формула для знаходження центру вписаного формули з 3 координатами (x₁, і₁), (x₂, і₂) і (x₃, і₃) є:

{(сокира ₁ + bx ₂ + cx ₃ )/(a + b + c), (є ₁ + від ₂ + c ₃ )/(a + b + c)}

Простіше кажучи, щоб отримати інцентр, ви:

• Помножте x-координату точки A на довжину сторони a, x-координату точки B на довжину сторони b і x-координату точки C на довжину сторони c. Потім додайте їх разом.
• Розділіть результат на суму довжин сторін a, b і c.
• Повторіть той самий процес для y-координат, але використовуючи довжини сторін a, b і c.

Формула вписаного кута трикутника

Формула для знаходження центру вписаного кута трикутника виглядає так:

Нехай у трикутнику D, F і G є точки, де бісектриси кутів A, B і C відповідно стикаються зі сторонами BC, AC і AB.

Кут ∠AIB (де I – центр вписаного трикутника) можна обчислити за формулою:

∠AIB = 180° – (половина суми кутів A і B)

АБО

∠AIB = 180° – (∠A + ∠B)/2

Як знайти центр вписання трикутника

Є два способи знайти центр вписаного трикутника. У побудові ми знаходимо центр вписаного трикутника, малюючи бісектриси кута трикутника. У координатній геометрії ми використовуємо формулу для визначення центру вписання.

Використання координатної геометрії : Знайдіть центр вписаного трикутника з координатами: A(2, 2), B(6, 2) і C(4, 5)

Відповідно до наданої інформації

• (х₁, і₁) = (2, 2)
• (х₂, і₂) = (6, 2)
• (х₃, і₃) = (4, 5)

Ми знаємо, що центр вписаного трикутника дорівнює:

I(x, y) = {(сокира ₁ + bx ₂ + cx ₃ )/(a + b + c), (є ₁ + від ₂ + c ₃ )/(a + b + c)}

Для сторони a: відстань між точками B і C = √((6 – 4)²+ (2 – 5)²) = √8

Для сторони b: відстань між точками A і C = √((2 – 4)²+ (2 – 5)²) = √13

Для сторони c: відстань між точками A і B = √((6 – 2)²+ (2 – 2)²) = 4

Підставляючи значення a, b, c у формулу вписаного центру, отримуємо:

I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4) )}

рядок для чату

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Центр вписаного трикутника ABC з координатами дорівнює (22/5,62/25)

Як побудувати центр вписаного трикутника?

Щоб побудувати центр вписаного трикутника, знадобиться циркуль. Використовуючи компас, виконайте наведені нижче дії.

Крок 1: Покладіть один кінець циркуля на вершину трикутника, а інший торкайтеся однієї сторони.

Крок 2: Використовуйте циркуль, щоб намалювати дві дуги з двох сторін трикутника.

крок 3: З однаковою відстанню за циркулем проведіть дві дуги всередині трикутника. Ці дуги повинні перетинати одна одну з того місця, де вони торкаються сторін.

крок 4: Проведіть лінію від вершини трикутника до місця перетину двох внутрішніх дуг.

крок 5: Повторіть ті ж дії з іншої вершини трикутника.

злиття, сортування java

Крок 6: Там, де дві лінії стикаються або перетинаються, знаходиться центр вписання трикутника.

Центр вписання прямокутного трикутника

Вписаний центр, якщо a Прямокутний трикутник це точка, де стикаються всі бісектриси кутів прямокутного трикутника. Якщо сторони прямокутного трикутника дорівнюють a, b і c, то радіус вписаного кола «r» подається як r = (ab)/(a + b + c). Вписаний центр прямокутного трикутника зображено нижче:

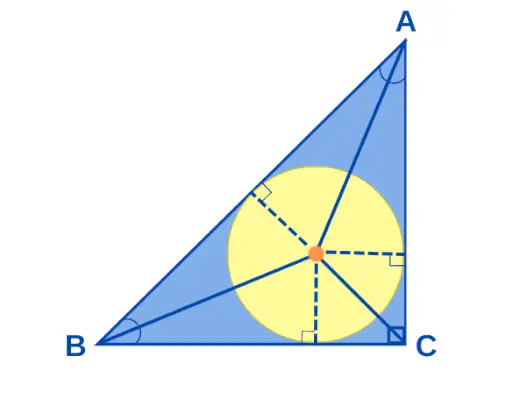
Центр вписання прямокутного трикутника

Центроїд, центр окружності, центр врізання, ортоцентр

Центроїд, центр окружності, центр вписання та ортоцентр — це чотири важливі точки, пов’язані з трикутником. Порівняння центроїда, центру окружності, центру врізання та ортоцентра наведено в таблиці нижче:

Також перевірте

• Площа трикутника
• Периметр трикутника
• Властивість суми кутів трикутника

Приклади вписаного центру трикутника

Приклад 1. Обчисліть центр вписаного трикутника ABC. AB= 8 см, BC= 15 см, CA= 17 см.

рішення:

Використовуючи формулу центру впису трикутника = (aA + bB + cC)/(a + b + c)

де,

• а = 8
• b = 15
• c = 17

А кути є,

• А = 30°
• B = 60°
• C = 90°

Додайте ці значення у формулу, щоб отримати,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Приклад 2: Джейн обчислила площу трикутного поля як 120 квадратних метрів. Периметр поля 36 метрів. Якщо коло накреслено всередині трикутника таким чином, що воно торкається кожної сторони трикутника, допоможіть Джейн обчислити внутрішній радіус трикутника.

рішення:

Згідно з наданою інформацією,

Площа трикутника = 120 кв

Периметр трикутника = 36 метрів

Ми знаємо, що площа трикутника = r × s

s = напівпериметр

s = p/2 = 36/2 = 18

A = r × s

r = А/с

r = 120/18

r = 6,67 метрів

Тренувальні задачі на центр вписаного трикутника

Завдання 1. Дано трикутник PQR з вершинами P(1, 2), Q(4, 6) і R(7, 2), знайдіть координати центру вписаного трикутника.

Завдання 2. Побудуйте трикутник ABC з ∠A = 45°, ∠B = 60° і ∠C = 75°. Використовуйте метод побудови, щоб знайти вписаний центр.

Завдання 3. У трикутнику LMN, якщо ∠L = 75°, ∠M = 60° і ∠N = 45°, знайдіть координати центру вписаного.

Завдання 4. Побудуйте трикутник XYZ з ∠X = 80°, ∠Y = 50° і ∠Z = 50°. Використовуйте метод побудови, щоб знайти вписаний центр.

Центр впису трикутника: поширені запитання

Що таке центр впису трикутника?

Центром вписаності трикутника є точка перетину бісектрис внутрішніх кутів. Він рівновіддалений від усіх трьох сторін трикутника.

Яке значення має центр вписаного трикутника?

Центр вписаного кола є важливим, оскільки він є центром кола, вписаного в трикутник, найбільшого кола, яке вміщується всередині трикутника. Він має властивість бути рівновіддаленим з усіх боків.

Чи може вписаний центр бути поза трикутником?

Ні, центр вписаного завжди знаходиться всередині трикутника. Це точка збігу бісектрис кута, і за визначенням вона має бути в межах трикутника.

Як будується центр розрізу за допомогою циркуля та прямої кромки?

Щоб побудувати вписаний центр, за допомогою циркуля проведіть бісектриси кута від кожної вершини до протилежної сторони. Центр вписування — це точка перетину цих бісектрис.

Що таке «Формула центру»?

Формулу центру впису трикутника можна записати так:

frac{(aA+bB+cC)}{a+b+c}

Які властивості має центр трикутника?

Інцентр має деякі ключові властивості. Він рівновіддалений від сторін трикутника, тобто відстані до сторін рівні. Крім того, це точка перетину бісектрис кутів, які ділять кути на дві рівні частини.

Як визначається Incentre?

Щоб визначити центр вписаного кута, потрібно знайти місце перетину бісектрис кута. Це можна зробити за допомогою формули вписаного центру або накресливши бісектриси кута та знайшовши точку їх перетину.

Яка різниця між центром центру та центром кола?

Основна відмінність між вписаним центром і окружним центром полягає в їх фокусі. Центр вписаного має справу з бісектрисами кута і є центром вписаного кола, тоді як центр описаного кола має справу з бісектрисами перпендикулярів і є центром описаного кола.

перший нащадок css

Інцентр і центроїд однакові?

Ні, вписаний центр і центроїд відрізняються. Центр вписаного кута - це місце, де стикаються бісектриси кута, тоді як центроїд - це місце, де перетинаються медіани. Медіани з'єднують вершини з серединою протилежної сторони.

Чи є Інцентр і Ортоцентр однаковими?

Ні, центр вписання та ортоцентр – це не те саме. Центр вписування — це точка, де кути ділять один одного навпіл, тоді як ортоцентр включає висоти — лінії, що від кожної вершини перпендикулярні до протилежної сторони. Це різні точки в трикутнику.