Жадібний метод є однією зі стратегій, таких як «Розділяй і володарюй», яка використовується для вирішення проблем. Цей метод використовується для вирішення задач оптимізації. Задача оптимізації - це задача, яка вимагає максимального або мінімального результату. Давайте розберемося через деякі терміни.
Метод Greedy є найпростішим і зрозумілим підходом. Це не алгоритм, а техніка. Основна функція цього підходу полягає в тому, що рішення приймається на основі наявної на даний момент інформації. Яка б поточна інформація не була в наявності, рішення приймається, не турбуючись про наслідки поточного рішення в майбутньому.
char + int у java
Цей метод в основному використовується для визначення можливого рішення, яке може бути або не бути оптимальним. Допустимим рішенням є підмножина, яка задовольняє заданим критеріям. Оптимальне рішення - це рішення, яке є найкращим і найсприятливішим рішенням у підмножині. У випадку здійсненних, якщо більш ніж одне рішення задовольняє заданим критеріям, тоді ці рішення будуть вважатися здійсненними, тоді як оптимальне рішення є найкращим рішенням серед усіх рішень.
Характеристика методу Greedy
Нижче наведено характеристики жадібного методу:
- Щоб побудувати рішення оптимальним чином, цей алгоритм створює два набори, де один набір містить усі вибрані елементи, а інший набір містить відхилені елементи.
- Алгоритм Greedy робить правильний локальний вибір у надії, що рішення має бути здійсненним або оптимальним.
Компоненти жадібного алгоритму
Компоненти, які можна використовувати в жадібному алгоритмі:
підрядок рядка java
Застосування жадібного алгоритму
- Він використовується для пошуку найкоротшого шляху.
- Він використовується для знаходження мінімального остовного дерева за допомогою алгоритму прима або алгоритму Крускала.
- Використовується в послідовності завдань із кінцевим терміном.
- Цей алгоритм також використовується для розв’язання задачі дробового рюкзака.
Псевдо код Greedy Algorithm
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Вище наведено жадібний алгоритм. Спочатку розв’язку присвоюється нульове значення. Ми передаємо масив і кількість елементів у жадібний алгоритм. Усередині циклу for ми вибираємо елементи один за одним і перевіряємо, чи є рішення можливим чи ні. Якщо рішення здійсненне, то виконуємо об’єднання.
Розберемося на прикладі.
Припустимо, що є проблема «P». Я хочу подорожувати від A до B, як показано нижче:
P : A → B
Проблема полягає в тому, що ми повинні пройти цю подорож від А до Б. Існують різні рішення, щоб пройти від А до Б. Ми можемо пройти від А до Б, пішки, машина, велосипед, потяг, літак , і т. д. У подорожі є обмеження, що ми маємо подолати цю подорож протягом 12 годин. Тільки якщо я їду поїздом або літаком, я можу подолати цю відстань протягом 12 годин. Існує багато рішень цієї проблеми, але є лише два рішення, які задовольняють обмеження.
Якщо ми говоримо, що ми повинні подолати дорогу з мінімальними витратами. Це означає, що ми повинні пройти цю відстань якомога менше, тому ця проблема відома як проблема мінімізації. Наразі ми маємо два можливих рішення, тобто одне потягом і інше повітрям. Оскільки подорож поїздом призведе до мінімальних витрат, це оптимальне рішення. Оптимальне рішення також є здійсненним рішенням, але забезпечує найкращий результат, так що це рішення є оптимальним рішенням з мінімальними витратами. Було б тільки одне оптимальне рішення.
Проблема, яка вимагає мінімального або максимального результату, називається проблемою оптимізації. Жадібний метод є однією зі стратегій, що використовуються для вирішення задач оптимізації.
як перетворити рядок на ціле число java
Недоліки використання алгоритму Greedy
Жадібний алгоритм приймає рішення на основі інформації, доступної на кожному етапі, без урахування ширшої проблеми. Отже, може існувати ймовірність того, що жадібне рішення не дає найкращого рішення для кожної проблеми.
Він дотримується локального оптимального вибору на кожному етапі з наміром знайти глобальний оптимум. Розберемося на прикладі.
містить python
Розгляньте графік, наведений нижче:
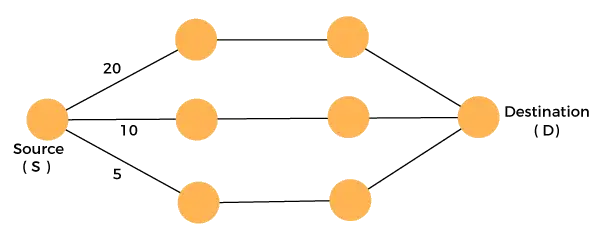
Ми повинні подорожувати від джерела до місця призначення з мінімальними витратами. Оскільки у нас є три можливих рішення, які мають шляхи витрат як 10, 20 і 5. 5 — шлях мінімальних витрат, тому це оптимальне рішення. Це локальний оптимум, і таким чином ми знаходимо локальний оптимум на кожному етапі, щоб обчислити глобальне оптимальне рішення.
