Враховуючи сітку чисел, знайти максимальну послідовність змії довжини та роздрукувати її. Якщо існує декілька послідовностей змії з максимальною довжиною друкувати будь -який з них.
Послідовність змії складається з сусідніх чисел у сітці, таким чином, що для кожного числа праворуч або числа, що знаходиться нижче, становить +1 або -1 його значення. Наприклад, якщо ви знаходитесь у розташуванні (x y) в сітці, ви можете або рухатися праворуч, тобто (x y+1), якщо це число ± 1, або рухатися вниз, тобто (x+1 y), якщо це число ± 1.
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Нижче на малюнку показані всі можливі шляхи:
gzip для Linux
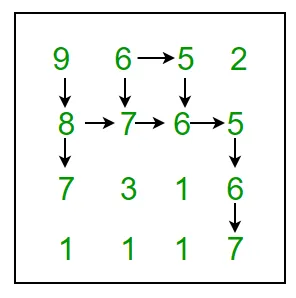
Ми настійно рекомендуємо вам мінімізувати свій браузер і спробувати це самостійно.
видалити файл в java
Ідея полягає у використанні динамічного програмування. Для кожної комірки матриці ми зберігаємо максимальну довжину змії, яка закінчується поточною коміркою. Максимальна послідовність змії довжини матиме максимальне значення. Максимальна комірка значення буде відповідати хвосту змії. Для того, щоб надрукувати змію, нам потрібно відступити від хвоста аж до голови змії.
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Нижче наведено реалізацію ідеї
C++// C++ program to find maximum length // Snake sequence and print it #include
// Java program to find maximum length // Snake sequence and print it import java.util.*; class GFG { static int M = 4; static int N = 4; static class Point { int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int grid[][] int mat[][] int i int j) { List<Point> path = new LinkedList<>(); Point pt = new Point(i j); path.add(0 pt); while (grid[i][j] != 0) { if (i > 0 && grid[i][j] - 1 == grid[i - 1][j]) { pt = new Point(i - 1 j); path.add(0 pt); i--; } else if (j > 0 && grid[i][j] - 1 == grid[i][j - 1]) { pt = new Point(i j - 1); path.add(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int mat[][]) { // table to store results of subproblems int [][]lookup = new int[M][N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.abs(mat[i - 1][j] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i - 1][j] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.abs(mat[i][j - 1] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i][j - 1] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } } } } System.out.print('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); System.out.print('Snake sequence is:'); for (Point it : path) System.out.print('n' + mat[it.x][it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void main(String[] args) { int mat[][] = {{9 6 5 2} {8 7 6 5} {7 3 1 6} {1 1 1 7}}; findSnakeSequence(mat); } } // This code is contributed by 29AjayKumar
// C# program to find maximum length // Snake sequence and print it using System; using System.Collections.Generic; class GFG { static int M = 4; static int N = 4; public class Point { public int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int[ ] grid int[ ] mat int i int j) { List<Point> path = new List<Point>(); Point pt = new Point(i j); path.Insert(0 pt); while (grid[i j] != 0) { if (i > 0 && grid[i j] - 1 == grid[i - 1 j]) { pt = new Point(i - 1 j); path.Insert(0 pt); i--; } else if (j > 0 && grid[i j] - 1 == grid[i j - 1]) { pt = new Point(i j - 1); path.Insert(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int[ ] mat) { // table to store results of subproblems int[ ] lookup = new int[M N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.Abs(mat[i - 1 j] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i - 1 j] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.Abs(mat[i j - 1] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i j - 1] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } } } } Console.Write('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); Console.Write('Snake sequence is:'); foreach(Point it in path) Console.Write('n' + mat[it.x it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void Main(String[] args) { int[ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence(mat); } } // This code is contributed by Princi Singh
def snakesequence(S m n): sequence = {} DP = [[1 for x in range(m+1)] for x in range(n+1)] a b maximum = 0 0 0 position = [0 0] for i in range(0 n+1): for j in range(0 m+1): a b = 0 0 p = 'initial' if(i > 0 and abs(S[i][j] - S[i-1][j]) == 1): a = DP[i-1][j] if(j > 0 and abs(S[i][j] - S[i][j-1]) == 1): b = DP[i][j-1] if a != 0 and a >= b: p = str(i-1) + ' ' + str(j) elif b != 0: p = str(i) + ' ' + str(j-1) q = str(i) + ' ' + str(j) sequence[q] = p DP[i][j] = DP[i][j] + max(a b) if DP[i][j] >= maximum: maximum = DP[i][j] position[0] = i position[1] = j snakeValues = [] snakePositions = [] snakeValues.append(S[position[0]][position[1]]) check = 'found' str_next = str(position[0]) + ' ' + str(position[1]) findingIndices = sequence[str_next].split() while(check == 'found'): if sequence[str_next] == 'initial': snakePositions.insert(0 str_next) check = 'end' continue findingIndices = sequence[str_next].split() g = int(findingIndices[0]) h = int(findingIndices[1]) snakeValues.insert(0 S[g][h]) snake_position = str(g) + ' ' + str(h) snakePositions.insert(0 str_next) str_next = sequence[str_next] return [snakeValues snakePositions] S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] m = 3 n = 3 seq = snakesequence(S m n) for i in range(len(seq[0])): print(seq[0][i] '' seq[1][i].split())
function snakesequence(S m n) { let sequence = {} let DP = new Array(n + 1) for (var i = 0; i <= n; i++) DP[i] = new Array(m + 1).fill(1) let a = 0 b = 0 maximum = 0 let position = [0 0] for (var i = 0; i <= n; i++) { for (var j = 0; j <= m; j++) { a = 0 b = 0 let p = 'initial' if(i > 0 && Math.abs(S[i][j] - S[i-1][j]) == 1) a = DP[i-1][j] if(j > 0 && Math.abs(S[i][j] - S[i][j-1]) == 1) b = DP[i][j-1] if (a != 0 && a >= b) p = String(i-1) + ' ' + String(j) else if (b != 0) p = String(i) + ' ' + String(j-1) let q = String(i) + ' ' + String(j) sequence[q] = p DP[i][j] = DP[i][j] + Math.max(a b) if (DP[i][j] >= maximum) { maximum = DP[i][j] position[0] = i position[1] = j } } } let snakeValues = [] let snakePositions = [] snakeValues.push(S[position[0]][position[1]]) let check = 'found' let String_next = String(position[0]) + ' ' + String(position[1]) let findingIndices = sequence[String_next].split(' ') while(check == 'found') { if (sequence[String_next] == 'initial') { snakePositions.unshift(String_next) check = 'end' continue } findingIndices = sequence[String_next].split(' ') let g = parseInt(findingIndices[0]) let h = parseInt(findingIndices[1]) snakeValues.unshift(S[g][h]) let snake_position = String(g) + ' ' + String(h) snakePositions.unshift(String_next) String_next = sequence[String_next] } return [snakeValues snakePositions] } // Driver Code let S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] let m = 3 let n = 3 let seq = snakesequence(S m n) for (var i = 0; i < seq[0].length; i++) console.log(seq[0][i] + '' seq[1][i].split(' '))
Випуск
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Складність часу вище розчину - O (M*n). Допоміжний простір, що використовується вищевказанням, є O (M*N). Якщо нам не потрібно друкувати простір змії, можна додатково зменшити до O (n), оскільки ми використовуємо лише результат з останнього рядка.
масив додавання елементів java
