приклад 1:
Розробіть NFA для таблиці переходів, як наведено нижче:
| Сучасний стан | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | д |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
рішення:
Діаграму переходу можна намалювати за допомогою функції відображення, наведеної в таблиці.
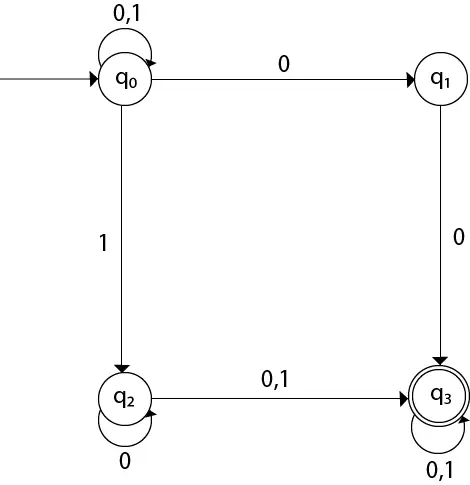
тут,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} приклад 2:
Розробка NFA з ∑ = {0, 1} приймає всі рядки, що закінчуються на 01.
статична функція в java
рішення:

Отже, NFA буде:

приклад 3:
Створіть NFA з ∑ = {0, 1}, у якому за подвійним «1» слідує подвійний «0».
рішення:
FA з подвійним 1 виглядає наступним чином:

Одразу слідує подвійний 0.
Потім,

Тепер перед подвійним 1 може бути будь-який рядок з 0 і 1. Так само, після подвійного 0 може бути будь-який рядок з 0 і 1.
Отже, NFA стає:

Тепер розглядаємо рядок 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Приклад 4:
Створіть NFA, у якому весь рядок містить підрядок 1110.
рішення:
Мова складається з усього рядка, що містить підрядок 1010. Діаграма часткового переходу може бути:

Тепер, оскільки 1010 може бути підрядком. Тому ми додамо вхідні 0 і 1, щоб можна було зберегти підрядок 1010 мови. Отже, NFA стає:
столи з латексу

Таблицю переходів для наведеної вище діаграми переходів можна навести нижче:
| Сучасний стан | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Розглянемо рядок 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Застряг! Оскільки для вхідного символу 0 немає шляху від q2. Ми можемо обробити рядок 111010 іншим способом.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Як стан q5 є прийнятним станом. Ми отримуємо повне сканування, і ми досягли кінцевого стану.
Приклад 5:
Розробка NFA з ∑ = {0, 1} приймає всі рядки, у яких третій символ з правого кінця завжди дорівнює 0.
рішення:

Таким чином ми отримуємо третій символ з правого кінця завжди як «0». NFA може бути:

Зображення вище є NFA, тому що в стані q0 із введенням 0 ми можемо перейти до стану q0 або q1.
