Передумова – інтелектуальний аналіз даних, міра подібності стосується відстані з розмірами, що представляють характеристики об’єкта даних у наборі даних. Якщо ця відстань менша, буде високий ступінь подібності, але коли відстань велика, буде низький ступінь подібності. Деякі з популярних заходів подібності:
- Евклідова відстань.
- Манхеттенська відстань.
- Подібність Жаккара.
- Відстань Мінковського.
- Косинус подібності.
Косинус подібність це метрика, яка допомагає визначити, наскільки схожі об’єкти даних, незалежно від їх розміру. Ми можемо виміряти подібність між двома реченнями в Python за допомогою косинусної подібності. У косинусній подібності об’єкти даних у наборі даних розглядаються як вектор. Формула для знаходження подібності косинуса між двома векторами:
(x, y) = x . y / ||x|| ||y||>
де,
- x . y = добуток (точка) векторів «x» і «y».||x|| і ||і|| = довжина (величина) двох векторів «x» і «y».||x||
||і|| = регулярний добуток двох векторів «x» і «y». приклад: Розглянемо приклад, щоб знайти подібність між двома векторами – «х» і 'та' , використовуючи косинусну подібність. Вектор «x» має значення, x = { 3, 2, 0, 5 } Вектор «y» має значення, y = { 1, 0, 0, 0 } Формула для обчислення косинусної подібності така: 
(x, y) = x. y / ||x|| ||і||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
Відмінність між двома векторами «x» і «y» визначається як –
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- Подібність косинуса між двома векторами вимірюється в «θ».
- Якщо θ = 0°, вектори «x» і «y» перекриваються, таким чином доводячи їх подібність.
- Якщо θ = 90°, вектори «x» і «y» є різними.
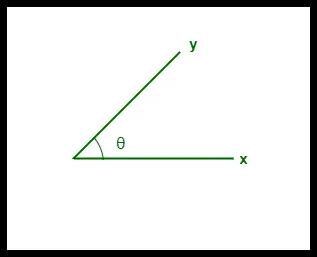
Косинус Подібність двох векторів
переваги:
- Косинусна подібність є корисною, оскільки навіть якщо два подібні об’єкти даних розташовані далеко один від одного на евклідову відстань через розмір, вони все одно можуть мати менший кут між собою. Чим менший кут, тим вище схожість.
- При нанесенні на багатовимірний простір подібність косинусів фіксує орієнтацію (кут) об’єктів даних, а не величину.