Імовірність карти — це ймовірність подій, що стосуються колоди гральних карт. Як ми знаємо, ймовірність є однією з важливих тем математики, яка займається обчисленням можливості будь-якої події. Простіше кажучи, ймовірність карти — це частина ймовірності, в якій ми знаходимо ймовірність вилучення карти з колоди карт. У цій статті ми дізнаємося про ймовірність карти з усіма подробицями про діаграму ймовірності карти, ймовірність гральної карти, як знайти ймовірність карти та розв’язані приклади ймовірності карти. Давайте почнемо наше навчання з теми ймовірності карти.
Що таке ймовірність?
Імовірність - це розділ математики, який вивчає можливість того, що будь-яка подія відбудеться чи ні. Математично це не що інше, як відношення кількості сприятливих результатів до загальної кількості результатів (простір вибірки) для події.
Деякі приклади ймовірності з реального життя:
- Граючи в карткові ігри, щоб знайти ймовірність виграшу або програшу в грі.
- Прогноз погоди, передбачити дощ.
- Результати виборів, щоб визначити, виграє чи програє кандидат.
- Результати іспиту, щоб визначити, складе чи провалить кандидат.
Формула ймовірності
Якщо E є подією з простором вибірки S, а кількість сприятливих результатів дорівнює n(E), тоді ймовірність події E, тобто P(E), визначається як:
P(E) = n(E) / n(S)
Що таке ймовірність карти?
Імовірність вилучення карти або колекції карт із колоди називається ймовірністю картки. Простими словами, ймовірність, пов'язана з гральними картами, називається картковою ймовірністю. Оскільки це тип ймовірності, він завжди лежить між 0 і 1. Наприклад, якщо нам потрібно знайти ймовірність витягнути туза з колоди карт, тобто 4/52 = 1/13 [Оскільки є 4 тузи в колоді 52 карти].
Колода карт у ймовірності
Колода карт — це колекція з 52 карт, які, здається, існують тисячі років. Вважається, що колода карт або гральні карти походять з Індії чи Китаю, перший задокументований доказ цих карт знайдено в 9тисКитай за часів династії Тан. Ці карти були схожі на сучасні карти і також поділені на чотири масті, але назва та символ цих мастей різні, тобто монети, рядки монет, міріади та міріади десятків.
У наш час ці карти мають різний дизайн і поділяються на чотири масті, а саме піку (♠), трефу (♣), черву (❤) і бубну (◆). Для однієї вибраної карти вибірковий простір становить 52, тобто загальна кількість результатів для однієї вибраної карти з колоди становить 52.
n(S) для колоди карт = 52
Типи карт у колоді
Будь-яку колоду карт можна класифікувати багатьма способами, деякі з параметрів, за якими можна класифікувати карти:
- На основі кольорів
- На основі костюмів
Давайте розберемося в цій класифікації докладніше наступним чином:
На основі кольорів
За кольорами колоду карт можна розділити на дві категорії:
- Червоні картки
- Чорні карти
Загалом 52 карти розділені порівну на червоні та чорні карти, тобто в колоді 26 червоних карт і 26 чорних карт.
На основі костюмів
У колоді карт чотири масті:
- Серця (❤)
- Діаманти (◆)
- Клуби (♣)
- Піки (♠)
Окрім цих, існує ще одна класифікація карт, заснована на ранзі карт:
- Туз
- Номерні картки
- Картки обличчя
Туз
Туз — це одна з таких карт, яка є або найважливішою, або найменш важливою в грі. На цій карті написано А, і в кожній масті є одна така карта, тобто чотири карти туза.
Номерні картки
Від 2 до 10 на одну масть припадає 9 карт, тобто всього таких карт 36.
Картки обличчя
Картки обличчя, як випливає з назви, містять фігуру або обличчя фігури на картці. Є три карти кожної масті, тобто валет, дама, король. Таким чином, загалом є 12 карт із обличчям.
Усі ці класифікації можна побачити в наступній таблиці.
| Колода карт (52 карти) | ||||
|---|---|---|---|---|
| Кольорові картки | Чорні карти (26 карт) | Червоні картки (26 карток) | ||
| Костюми | Піка (13 карт) | Трефа (13 карток) | Серце (13 карток) | Алмаз (13 карт) |
| Картки обличчя (12 карт у колоді та по 3 карти кожної масті) | К (король) | К (король) | К (король) | К (король) |
| Q (королева) | Q (королева) | Q (королева) | Q (королева) | |
| J (Джек) | J (Джек) | J (Джек) | J (Джек) | |
| Номерні картки (36 карт в колоді і 9 карт в одній масті) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Карти туза (4 карти в колоді і 1 карта в одній масті) | A (туз) | A (туз) | A (туз) | A (туз) |
Таблиця колоди карт
Наступна таблиця представляє класифікацію колоди гральних карт:
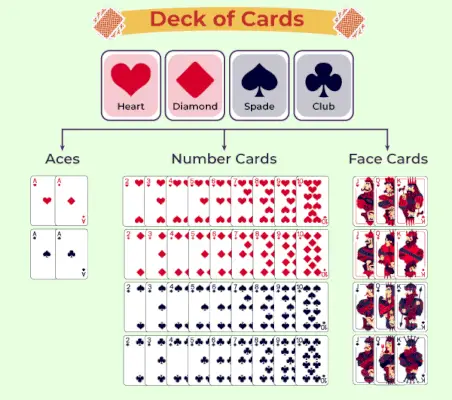
Ймовірність гральних карт
Деякі з поширених подій у ймовірності карт обговорюються в наступній таблиці:
| Подія E для розіграшу картки | Імовірність P(E) |
|---|---|
| Туз | P(E) = 4/52 = 1/13 |
| Король | P(E) = 4/52 = 1/13 |
| Номер картки | P(E) = 36/52 = 9/13 |
| Картка обличчя | P(E) = 12/52 = 3/13 |
| Пікова карта | P(E) = 13/52 = 1/4 |
| Червона картка | P(E) = 26/52 = 1/2 |
Як знайти ймовірність карт?
Кроки для визначення ймовірності подій, що включають картки, такі ж, як і для всіх інших ймовірностей, які наведені таким чином:
Крок 1: Спочатку знайдіть кількість сприятливих результатів із заданого запитання.
ряд фібоначчі в javaКрок 2: Потім знайдіть загальну кількість результатів.
крок 3: Застосуйте формулу ймовірності, щоб знайти ймовірність картки.
Приклад: яка ймовірність витягнути туза з колоди карт?
відповідь:
Тут Е — подія вилучення карти туза
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = вилучення карти туза з колоди = 4 (в 1 колоді 4 карти туза)
P(E) = n(E) / n(S) = 4 / 52
P(E) = 1/13
Ймовірність взяти карту туза = 1/13
Приклади запитань про ймовірність карти
Завдання 1: Яка ймовірність вилучення наступних карт із колоди карт?
(i) піку
(ii) чорна картка
(iii) картку з номером
рішення:
(i) Тут E — подія витягування пікової карти
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = взяття пікової карти з колоди = 13 (в 1 колоді 13 карт кожної масті)
P(E) = n(E) / n(S) = 13 / 52
P(E) = 1/4
Імовірність витягнути піку = 1/4
(ii) Тут E — подія вилучення чорної картки
Загальна кількість результатів у колоді n(S) = 52
Шрифти для gimpКількість сприятливих результатів = n(E) = вилучення чорної карти з колоди = 26 (в 1 колоді 26 чорних карт)
P(E) = n(E) / n(S) = 26 / 52
P(E) = 1/2
Ймовірність витягнути чорну картку = 1/2
(iii) Тут E — подія витягування картки з номером
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = вилучення картки з цифрами з колоди = 36 (в 1 колоді 36 карток з цифрами)
P(E) = n(E) / n(S) = 36 / 52
P(E) = 9/13
Імовірність вилучення картки з числом = 9/13
Завдання 2: Яка ймовірність взяти наступні карти з колоди карт?
(i) Король або чорна карта
(ii) Червона картка з тузом
рішення:
(i) Тут E — подія вилучення короля або чорної карти
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = взяття короля або чорної карти з колоди = 26 + 2 = 28 (В 1 колоді є 26 чорних карт, у яких 2 короля та 2 чорних короля)
P(E) = n(E) / n(S) = 28 / 52
P(E) = 7/13
Ймовірність взяти короля або чорну карту = 7/13
(іі) Тут E — це подія вилучення червоної карти з тузом
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = вилучення червоної карти з тузом з колоди = 2 (Є 26 червоних карток, у яких 2 карти туза)
Відповідно до запитання витягнута карта має бути червоною та тузом. Отже, n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1/26
Ймовірність взяти червону картку з тузом = 1/26
Завдання 3: Яка ймовірність вилучення наступних карт із колоди карт?
(i) Неклубна картка
(ii) Нелицьова картка
рішення:
(i) Тут E — подія витягування неклубної карти
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = взяття нетрефової карти з колоди = 39 (в 1 колоді 13 треф, неколода = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39 / 52
P(E) = 3/4
Ймовірність взяти неклубну карту = 3/4
(ii) Тут E — подія витягування нелицьової карти
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = вилучення нелицьової карти з колоди = 40 (в 1 колоді 12 лицьових карт, неколода = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40 / 52
P(E) = 10/13
Ймовірність взяти неклубну карту = 10/13
Проблема 4: Яка ймовірність взяти картку, яка не є ні червоною, ні особою?
рішення:
Тут E — подія витягування ні червоної, ні лицьової картки
Загальна кількість результатів у колоді n(S) = 52
Кількість сприятливих результатів = n(E) = не взяти з колоди ні червону, ні лицьову карту.
Всього червоних карток = 26
Всього в колоді 12 карт із обличчям, але 6 червоних карт із обличчям уже видалено. Таким чином, залишилося карток із лицьовою стороною = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/52
P(E) = 8/13
Ймовірність витягнути картку, яка не має ні червоного, ні лицьового кольору = 8/13
Задача 5: Яка ймовірність взяти дві карти з колоди карт із заміною, якщо перша карта — серце, а друга — бубн?
рішення:
Ймовірність витягнути першу картку як серце = 13/52
оператор switch javaПісля витягнення першої карти картку видаляють.
Імовірність взяти другу карту як бубн = 13/51
Ймовірність витягнути першу картку як серце, а другу як діамант = (13 / 52) × (13 / 51)
Імовірність витягнути першу картку як серце, а другу як ромб = 13/204
Поширені запитання про ймовірність карти
1. Що таке ймовірність карти?
Ймовірність вилучення карти з колоди карт називається ймовірністю карти.
2. Перелічіть типи мастей у колоді карт.
У колоді карт є чотири види мастей. Вони є:
- Серця
- Діаманти
- Піки
- клуби
3. Який вибірковий простір для колоди карт, коли одна карта витягнута з колоди?
Зразок місця для колоди карт, коли витягнуто одну карту, містить 52 результати.
4. Напишіть формулу для знаходження ймовірності.
Формула для обчислення ймовірності визначається так:
Імовірність події = кількість сприятливих подій / загальна кількість результатів
АБО
P(E) = n(E) / n(S)
5. Скільки карт із обличчям у колоді карт?
У колоді карт є 12 карт із обличчями.
