- Побітовий оператор XOR також відомий як Виключне АБО
- Його позначають за допомогою '^'
- Як видно з назви, він працює на бітовий рівень операндів.
- Побітовий оператор XOR відноситься до категорії побітових операторів.
- У побітовому виключаючому операторі АБО (XOR) потрібні два операнди, і ці два операнди розділені символом XOR, тобто «^».
- Щоб визначити вихід або результат, який виходить після застосування оператора XOR до двох операндів, нам потрібно слідувати таблиці логічної істинності оператора XOR.
- Таблиця істинності XOR — це математична таблиця, побудована за допомогою відповідної логіки оператора XOR.
- Логіка, яка використовується за оператором XOR: щоразу, коли операція XOR застосовується до двох інший бітів двох операндів, то результат буде видаватись завжди '1', і якщо операція XOR застосовується до двох те саме біти двох операндів, тоді результат дає вихід '0'.
Таблиця істинності оператора виняткового АБО (XOR).
Нехай є два операнди; Перший — A, а другий — B, загальна кількість вхідних даних, утворених цими двома операндами, становитиме 4. Використовуючи наступну таблицю істинності XOR, ми визначимо відповідний вихід. Результат буде записано на C тут C = A ^ B.
У цій таблиці істинності ми приймаємо вхідні дані у формі бітів, тобто 0 і 1, і вихідні дані також будуть згенеровані у формі бітів, тобто 0 і 1.
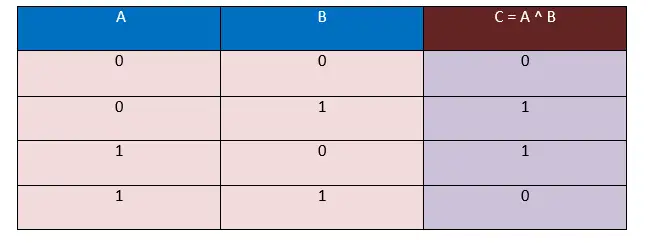
Тут, у наведеній вище таблиці істинності XOR, ми спостерігаємо, що коли значення операндів A і B різні, тобто (0, 1), (1, 0), результат, який виходить, завжди буде 1. І коли значення операндів A і B однакові, тобто ( 0, 0 ), ( 1, 1 ), результат, який виходить, завжди буде 0.
Подібним чином, таким чином, ми можемо намалювати таблицю істинності для Логічний цінності -
Нехай є два операнди; перший є А а другий є Б . Загальна кількість комбінацій вхідних даних, утворених цими двома операндами, становитиме 4. Використовуючи наступну таблицю істинності XOR, ми визначимо відповідний вихід. Результат буде записано в C, тут C = A ^ B.
У цій таблиці істинності ми вводимо дані у формі значень Truth, тобто True (T) і False (F). Вихідні дані також будуть згенеровані у формі справжніх значень, тобто T і F.

Тут, у наведеній вище таблиці істинності XOR, ми спостерігаємо, що коли значення операндів A і B різні, тобто (F, T), (T, F), результатом завжди буде T. І коли значення операндів A і B однакові, тобто (F, F), (T, T), результатом завжди буде F.
З наведених вище таблиць ми це бачимо T ( True ) позначається одиницею, а F ( False ) позначається 0.
Кроки для вирішення будь-якої проблеми -
- Операнди, подані в задачі, завжди будуть мати десяткове значення.
- По-перше, нам потрібно перетворити значення операндів у двійковий
- Після перетворення значень операндів у двійкові числа помістіть обидва операнди один над одним.
- Пам’ятайте, що перед застосуванням до них операції ексклюзивного АБО (XOR), перевірте кількість цифр у них.
- Якщо кількість цифр не збігається, додаткові 0 у лівому кінці малого операнда врівноважують кількість цифр.
- Нарешті, за допомогою наведеної вище таблиці істинності застосуйте операнд XOR до операндів один за одним, беручи по одному біту для застосування операції XOR.
- Нарешті, результат виробляється у вигляді виходу.
- Вихідні дані будуть у двійковій формі, тепер перетворіть двійкову форму в десяткову та запишіть отримане значення.
Виконання операції побітового виключного АБО (XOR) у C++
Розберемося більш детально з виконанням операції XOR в C++ на прикладах -
Приклад 1: знайти виключне АБО цілих значень; 10 і 14. Крім того, поясніть це та напишіть код виконання на C++.
рішення: Розглянемо дві змінні, 'a' і 'b', щоб зберегти відповідні два операнди, наведені у запитанні вище, тобто 10 і 14.
Тут a = 10 і b = 14.
Ми виконаємо наведені нижче кроки, щоб знайти виключне АБО наведених двох операндів.
- Ми знаємо, що 10 і 14 мають десяткову форму, і для застосування порозрядної операції XOR необхідно перетворити її в двійкову форму.
- Двійкова форма 'a', тобто 10 є '1010' і двійкова форма 'b', тобто 14 є '1110'.
- Тут ми спостерігаємо, що кількість двійкових цифр у a дорівнює чотирьом, а кількість двійкових цифр у b також дорівнює 4; отже, кількість двійкових цифр, присутніх в обох змінних, є однаковою і вже збалансованою, нам не потрібно додавати ще кількість 0, щоб збалансувати це.
- Тепер помістимо двійкові цифри в «b» до двійкових цифр у «a».
- Нарешті, застосовуючи операцію XOR один за одним до відповідних бітів, які збігаються та записують результат.
- Нарешті згенерований результат буде у двійковій формі, оскільки запитання вище подано у десятковій формі, тому нам потрібно перетворити результат у десяткову форму.
Пояснення:
a = 10 (у десятковій формі)
b = 14 (у десятковій формі)
Тепер, для XOR b, нам потрібно перетворити a і b у двійкову форму -
a = 1010 (у двійковій формі)
b = 1110 (у двійковій формі)
Тепер застосовуючи операцію XOR до a і b -
а = 1010
b = 1110
---------------
a ^ b = 0100 (У двійковій формі)
Результатом a ^ b є 0100 у двійковій формі.
Тепер конвертуємо результат у десяткову форму, тобто 4.
10^14 = 4
ПРИМІТКА. Використовуючи наведену вище таблицю істинності XOR, генеруються вихідні дані відповідних бітів.
Тепер ми застосуємо порозрядну операцію XOR до 10 і 14 мовою C++ і отримаємо результат, тобто 4.
Код C++ для прикладу вище:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Вихід

Приклад 2: знайти виключне АБО цілих значень; 3 і 15. Також поясніть це та напишіть код виконання на C++.
рішення: Розглянемо дві змінні, 'a' і 'b', щоб зберегти відповідні два операнди, наведені у запитанні вище, тобто 3 і 15.
Тут a = 3 і b = 15.
Ми виконаємо наведені нижче кроки, щоб знайти виключне АБО наведених двох операндів.
- Ми знаємо, що 3 і 15 знаходяться в десятковій формі, і для застосування порозрядної операції XOR необхідно перетворити її в двійкову форму.
- Двійкова форма 'a', тобто 3 є 'одинадцять' і двійкова форма 'b', тобто 15 є '1111'.
- Тут ми зауважимо, що кількість двійкових цифр у a дорівнює двом, а кількість двійкових цифр у b дорівнює чотирьом; отже кількість двійкових цифр, присутніх в обох змінних, неоднакова. Таким чином, якщо незбалансовано, нам потрібно додати більше нулів ліворуч від молодшого двійкового числа, тобто a, яке є ' одинадцять , щоб збалансувати його.
- Після балансування значення a дорівнює '0011' , і b є '1111'.
- Тепер помістимо двійкові цифри в 'b' до двійкових цифр в 'a'.
- Нарешті, застосовуючи операцію XOR один за одним до відповідних бітів, які збігаються та записують результат.
- Нарешті згенерований результат буде у двійковій формі, оскільки запитання вище подано у десятковій формі, тому нам потрібно перетворити результат у десяткову форму.
Пояснення:
підрядок методу java
a = 3 (у десятковій формі)
b = 15 (у десятковій формі)
Тепер, для XOR b, нам потрібно перетворити a і b у двійкову форму -
a = 0011 (у двійковій формі)
b = 1111 (у двійковій формі)
Тепер застосовуючи операцію XOR до a і b -
а = 0011
b = 1111
---------------
a ^ b = 1100 (У двійковій формі)
Результатом a ^ b є 1100 у двійковій формі.
Тепер конвертуємо результат у десяткову форму, тобто 12.
3^15 = 12
ПРИМІТКА. Використовуючи наведену вище таблицю істинності XOR, генеруються вихідні дані відповідних бітів.
Тепер ми застосуємо порозрядну операцію XOR до 3 і 15 мовою C++ і отримаємо результат, тобто 12.
Код C++ для прикладу вище:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Вихід

