Відро сортування це техніка сортування, яка передбачає розподіл елементів на різні групи або відра. Ці ковші утворюються шляхом рівномірного розподілу елементів. Коли елементи розділені на сегменти, їх можна відсортувати за допомогою будь-якого іншого алгоритму сортування. Нарешті, відсортовані елементи збираються разом у впорядкованому порядку.
Алгоритм сортування сегментів:
Створити п порожні відра (або списки) і виконайте наступні дії для кожного елемента масиву arr[i].
- Вставте arr[i] у відро [n*array[i]]
- Сортуйте окремі сегменти за допомогою сортування вставкою.
- Об’єднайте всі відсортовані відра.
Як працює Bucket Sort?
Щоб застосувати групове сортування до вхідного масиву [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , ми виконуємо такі кроки:
Крок 1: Створіть масив розміром 10, де кожен слот представляє відро.

Створення відер для сортування
крок 2: Вставте елементи в сегменти з вхідного масиву на основі їх діапазону.
Вставка елементів у відра:
- Візьміть кожен елемент із вхідного масиву.
- Помножте елемент на розмір масиву ковшів (у цьому випадку 10). Наприклад, для елемента 0,23 ми отримуємо 0,23 * 10 = 2,3.
- Перетворіть результат на ціле число, яке дасть нам індекс відра. У цьому випадку 2,3 перетворюється на ціле число 2.
- Вставте елемент у відро, що відповідає розрахованому індексу.
- Повторіть ці кроки для всіх елементів у вхідному масиві.
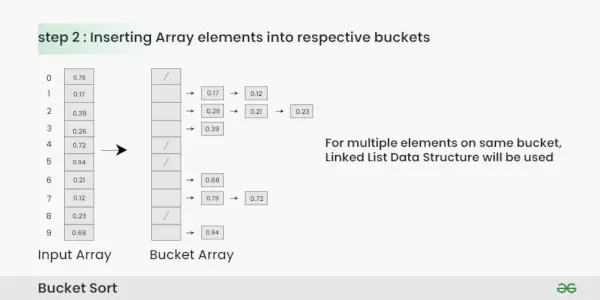
Вставлення елементів масиву у відповідні сегменти
крок 3: Відсортуйте елементи в кожному відерці. У цьому прикладі ми використовуємо швидке сортування (або будь-який стабільний алгоритм сортування) для сортування елементів у кожному сегменті.
Сортування елементів у кожному сегменті:
- Застосуйте стабільний алгоритм сортування (наприклад, бульбашкове сортування, сортування злиттям), щоб сортувати елементи в кожному сегменті.
- Елементи в кожному сегменті тепер відсортовано.
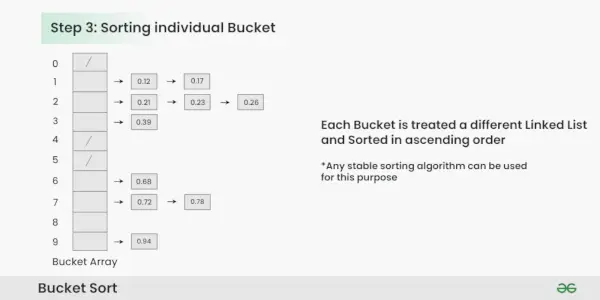
Сортування окремого відра
лисиця проти вовка
крок 4: Зберіть елементи з кожного відра та помістіть їх назад у вихідний масив.
Збір елементів з кожного відра:
- Перейдіть по кожному сегменту по порядку.
- Вставте кожен окремий елемент із відра у вихідний масив.
- Після того, як елемент скопійовано, він видаляється з відра.
- Повторіть цей процес для всіх відер, доки всі елементи не будуть зібрані.
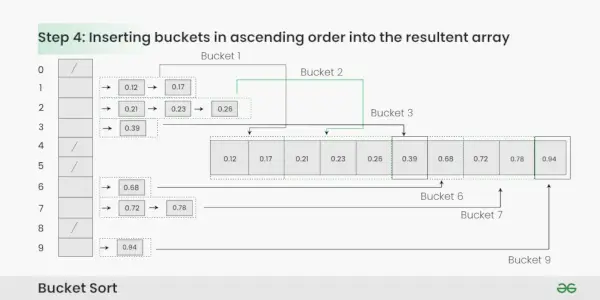
Вставка сегментів у порядку зростання в отриманий масив
крок 5: Початковий масив тепер містить відсортовані елементи.
Остаточний відсортований масив із використанням ковшового сортування для заданого введення: [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].

Повернути відсортований масив
Реалізація алгоритму ковшового сортування:
Нижче наведено реалізацію Bucket Sort:
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& bucket) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> ключ) { bucket[j + 1] = bucket[j]; j--; } bucket[j + 1] = ключ; } } // Функція сортування arr[] розміром n за допомогою сортування сегментів void bucketSort(float arr[], int n) { // 1) Створити n порожніх векторів сегментівb[n]; // 2) Розмістіть елементи масиву в різних сегментах для (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listвідро) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && bucket.get(j)> ключ) { bucket.set(j + 1, bucket.get(j)); j--; } bucket.set(j + 1, ключ); } } // Функція сортування arr[] розміром n за допомогою сортування сегментів public static void bucketSort(float[] arr) { int n = arr.length; // 1) Створіть n порожніх списків відер[] відра = новий ArrayList[n]; для (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 і bucket[j]> ключ: bucket[j + 1] = bucket[j] j -= 1 bucket[j + 1] = ключ def bucket_sort(arr): n = len(arr) bucket = [[] for _ in range(n)] # Розмістіть елементи масиву в різних відрах для num в arr: bi = int(n * num) buckets[bi].append(num) # Сортуйте окремі відра за допомогою сортування вставкою для відра у відрах: insertion_sort (bucket) # Об’єднати всі відра в arr[] index = 0 для відра у відрах: для num у відрі: arr[index] = num index += 1 arr = [0,897, 0,565, 0,656, 0,1234, 0,665, 0,3434] bucket_sort (arr) print('Відсортований масив:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listвідро) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> ключ) { bucket[j + 1] = bucket[j]; j--; } bucket[j + 1] = ключ; } } // Функція сортування arr[] розміром n за допомогою сортування сегментів static void BucketSort(float[] arr) { int n = arr.Length; // 1) Створіть n порожніх списків відер[] відра = новий список[n]; для (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Розмістіть елементи масиву в різних сегментах для (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && bucket[j]> ключ) { bucket[j + 1] = bucket[j]; j--; } bucket[j + 1] = ключ; } } функція bucketSort(arr) { let n = arr.length; let buckets = Array.from({length: n}, () => []); // Помістіть елементи масиву в різні сегменти для (let i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Вихід
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Аналіз складності алгоритму сортування сегментів:
Часова складність: O(n2),
- Якщо ми припустимо, що вставлення у відро займає O(1) часу, то кроки 1 і 2 наведеного вище алгоритму однозначно займають O(n) часу.
- O(1) легко можливий, якщо ми використовуємо пов’язаний список для представлення відра.
- Крок 4 також займає O(n) часу, оскільки у всіх сегментах буде n елементів.
- Основним кроком для аналізу є крок 3. Цей крок також займає в середньому O(n) часу, якщо всі числа рівномірно розподілені.
Допоміжний простір: O(n+k)
