Двійкова система числення це система числення, яка використовується для представлення різних чисел за допомогою лише двох символів 0 і 1. Слово двійковий походить від слова bi, що означає два. Тому цю систему числення називають двійковою. Таким чином, двійкова система числення — це система, яка має лише два символи.
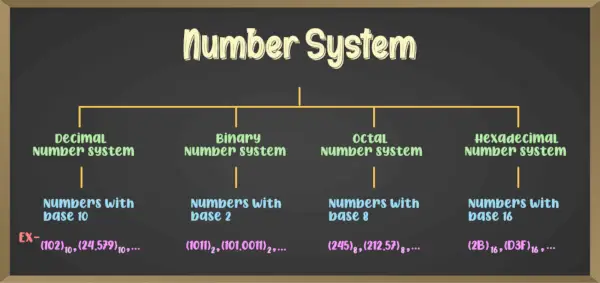
Загалом існують різні типи систем числення, серед яких чотири основні:
- Двійкова система числення (система числення з основою 2)
- Вісімкова система числення (система числення з основою 8)
- Десяткова система числення (система числення з основою 10)
- Шістнадцяткова система числення (система числення з основою 16)
Тут ми лише дізнаємося про двійкову систему числення. Ця система числення дуже корисна для пояснення завдань на комп’ютері. У двійковій системі числення ми маємо два стани 0 і 1, і ці два стани представлені двома станами транзистора. Якщо струм проходить через транзистор, комп’ютер читає 1, а якщо струм відсутній на транзисторі, він читає 0. Таким чином, змінюючи струм, комп’ютер читає двійкову систему числення. Кожен розряд у двійковій системі числення називається бітом.
У цій статті ми детально дізнаємося про двійкову систему числення, перетворення двійкової системи числення, двійкову таблицю, роботу з двійковими числами, приклади та ін.
Зміст
- Двійкова система числення
- Таблиця двійкових чисел
- Перетворення двійкової системи в десяткову
- Перетворення десяткової системи в двійкову
- Арифметичні дії над двійковими числами
- 1 і 2 доповнення до двійкового числа
- Використання двійкової системи числення
- Приклад двійкової системи числення
Двійкова система числення
Двійкова система числення — це система числення, в якій ми використовуємо дві цифри 0 і 1 для виконання всіх необхідних операцій. У двійковій системі числення ми маємо основу 2. Основу двійкової системи числення також називають основою числа. система числення .
У двійковій системі числення ми представляємо число як
- (11001)2
У наведеному вище прикладі наведено двійкове число, основа якого дорівнює 2. У двійковій системі числення кожна цифра називається бітом. У наведеному вище прикладі 5 цифр.
Таблиця двійкових чисел
| Десяткове число | Двійкове число | Десяткове число | Двійкове число |
|---|---|---|---|
| 1 | 001 | одинадцять | 1011 |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | п'ятнадцять | 1111 |
| 6 | 110 наприклад ім'я користувача | 16 | 10000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 | 1010 | двадцять | 10100 |
Перетворення двійкової системи в десяткову
Двійкове число перетворюється на десяткове шляхом множення кожної цифри двійкового числа на ступінь 1 або 0 до відповідного ступеня 2. Припустімо, що двійкове число має n цифр, B = an-1…а3a2a1a0. Тепер відповідне десяткове число подано як
D = (а n-1 ×2 n-1 ) +…+(а 3 ×2 3 ) + (а 2 ×2 2 ) + (а 1 ×2 1 ) + (а 0 ×2 0 )
Розглянемо приклад, щоб краще зрозуміти концепцію.
Приклад: конвертувати (10011) 2 до десяткового числа.
рішення:
Дане двійкове число (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Отже, двійкове число (10011)2виражається як (19)10.
Перетворення десяткової системи в двійкову
Десяткове число перетворюється на двійкове шляхом безперервного ділення заданого десяткового числа на 2, доки ми не отримаємо частку як 1, і ми записуємо числа знизу вгору.
Розглянемо приклад, щоб краще зрозуміти концепцію.
Приклад: конвертувати (28) 10 у двійкове число.
рішення:
Отже, (28)10виражається як (11100)2.
Арифметичні дії над двійковими числами
Ми можемо легко виконувати різні операції з двійковими числами. Різні арифметичні операції над двійковими числами включають:
- Двійкове додавання
- Двійкове віднімання
- Двійкове множення
- Двійковий поділ
Тепер дізнаємося про те ж докладніше.
Двійкове додавання
Результат додавання двох двійкових чисел також є двійковим числом. Щоб отримати результат додавання двох двійкових чисел, потрібно додати цифру двійкових чисел за цифрою. У доданій нижче таблиці показано правило двійкового додавання.
| Двійкове число (1) | Двійкове число (2) | Доповнення | нести |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Двійкове віднімання
Результат віднімання двох двійкових чисел також є двійковим числом. Щоб отримати результат віднімання двох двійкових чисел, потрібно відняти цифру двійкових чисел за цифрою. Таблиця, додана нижче, показує правило двійкового віднімання.
| Двійкове число (1) | Двійкове число (2) | Віднімання | Позичити |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Двійкове множення
Процес множення двійкових чисел подібний до множення десяткових чисел. Правила множення будь-яких двох двійкових чисел наведені в таблиці,
| Двійкове число (1) іменування правил java | Двійкове число (2) | Множення |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Двійковий поділ
The метод ділення для двійкових чисел подібний до методу десяткового ділення чисел. Розглянемо приклад, щоб краще зрозуміти концепцію.
Приклад: розділити (101101) 2 від (110) 2
рішення:
Доповнення двійкового числа до 1 і 2
- Доповнення двійкового числа до 1 отримують інвертуванням цифр двійкового числа.
Приклад: знайдіть доповнення до 1 до (10011) 2 .
рішення:
Дане двійкове число (10011)2
Тепер, щоб знайти доповнення до 1, нам потрібно перевернути цифри даного числа.
Таким чином, доповнення до 1 до (10011)2є (01100)2
- Доповнення двійкового числа до 2 отримується інвертуванням цифр двійкового числа, а потім додаванням 1 до молодшого біта.
Приклад: знайдіть доповнення до 2 до (1011) 2 .
рішення:
Задане двійкове число (1011)2
Щоб знайти доповнення до 2, спочатку знайдіть його доповнення до 1, тобто (0100)2
Тепер, додавши 1 до молодшого біта, ми отримаємо (0101)2
Отже, доповнення 2 до (1011)2є (0101)2
Використання двійкової системи числення
Двійкові системи числення використовуються для різних цілей, і найважливішим використанням двійкової системи числення є,
- Двійкова система числення використовується в усій цифровій електроніці для виконання різноманітних операцій.
- Мови програмування використовують двійкову систему числення для кодування та декодування даних.
- Двійкова система числення використовується в науках про дані для різних цілей тощо.
Детальніше,
- Двійкова формула
- Різниця між десятковою та двійковою системами числення
Приклад двійкової системи числення
Приклад 1: Перетворення десяткового числа (98) 10 у двійковий формат.
рішення:
Таким чином, двійкове число для (98)10дорівнює (1100010)2
Приклад 2: Перетворення двійкового числа (1010101) 2 до десяткового числа.
рішення:
Дане двійкове число, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 × 26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Таким чином, двійкове число (1010101)2дорівнює (85)10в десятковій системі числення.
Приклад 3: Розділ (11110) 2 від (101) 2
рішення:
Приклад 4: Додати (11011) 2 і (10100) 2
рішення:
Отже, (11011)2+ (10100)2= (101111)2
Приклад 5: віднімання (11010) 2 і (10110) 2
рішення:
Отже, (11010)2– (10110)2= (00100)2
Приклад 6: Множення (1110) 2 і (1001) 2 .
символ в int java
рішення:
Таким чином, (1110)2× (1001)2= (1111110)2
Поширені запитання про двійкову систему числення
Що таке двійкова система числення?
Двійкова система числення — одна з чотирьох систем числення, яка використовується для представлення чисел за допомогою лише двох цифр, 0 і 1. У двійковій системі числення цифри називаються «бітами». Двійкова система числення використовується комп’ютерами для виконання різноманітних обчислень.
Що таке a Б це?
Біт у двійковій системі числення визначається як окрема цифра, яка містить значення «0» або «1».
Що таке Ніббл?
Група з чотирьох цифр називається Niblle.
Що таке двійкове значення 10?
Двійкове значення 10 дорівнює (1010)2
Які існують типи систем числення?
Існують різні типи систем числення, і деякі з них:
- Двійкова система числення
- Вісімкова система числення
- Десяткова система числення
- Шістнадцяткова система числення
Як обчислити двійкові числа?
Двійкові числа обчислюються з дворядних чисел шляхом ділення десяткового числа на 2 і запису залишку. Потім ми розташовуємо всі залишки від найновішого до найстаршого, щоб отримати двійкове число.
Як додати двійкові числа?
Двійкові числа складаються за допомогою наведених нижче формул:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (перенесення 1)






